Description

This function displays $d_{z}$ for Z-tests based on the Z-statistic. The normal confidence interval is also provided if you have sigma ($\sigma$). If “sig” is left blank, then you will not see a confidence interval.

The formula for $d_{z}$ is: $$d_{z} = \frac{Z}{\sqrt(N)}$$

The formula for $d_{z}$ is: $$d_{z} = \frac{M - \mu}{\sigma_M}$$

R Function

d.z.z(z, sig = NA, n, a = 0.05)

Arguments

  • z = statistic
  • sig = population standard deviation
  • n = sample size
  • a = significance level

Example

A recent study suggested that students (N = 100) learning statistics improved their test scores with the use of visual aids (Z = 2.50, SD = 4.00).

Function in R:

d.z.z(z = 2.5, sig = 4, n = 100, a = .05)

MOTE

Screenshot

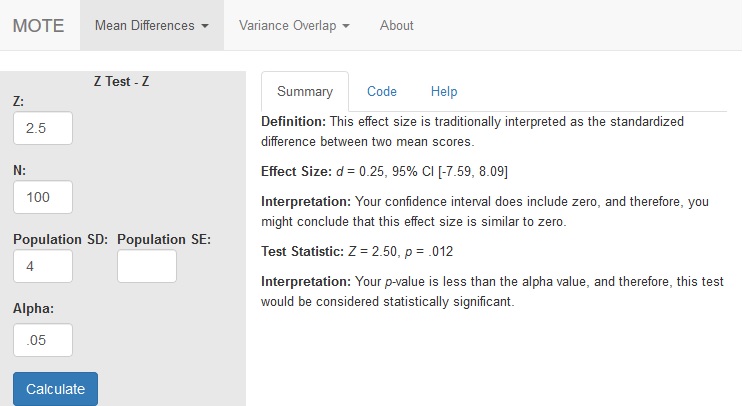
Z-Test - Z Screenshot

Effect Size:

Effect Size: $d_{z}$ = 0.25, 95% CI [-7.59, 8.09]

Interpretation:

Your confidence interval does include zero, and therefore, you might conclude that this effect size is similar to zero.

Summary Statistics:

Not applicable.

Test Statistic:

Z = 2.50, p = .012

Interpretation:

Your p-value is less than the alpha value, and therefore, this test would be considered statistically significant.

Tutorial