Description

This function displays epsilon squared from ANOVA analyses and its non-central confidence interval based on the F distribution. This formula works for one way and multi way designs with careful focus on the sum of squares total calculation.

The formula for $\epsilon^2$ is: $$\frac{df_{model} \times (MS_{model} - MS_{error})} {SS_{total}}$$

The formula for F is: $$\frac{MS_{model}}{MS_{error}}$$

R Function

epsilon.full.SS(dfm, dfe, msm, mse, sst, a = 0.05)

Arguments

  • dfm = degrees of freedom for the model/IV/between
  • dfe = degrees of freedom for the error/residual/within
  • msm = mean square for the model/IV/between
  • mse = mean square for the error/residual/within
  • sst = sum of squares total
  • a = significance level

Example

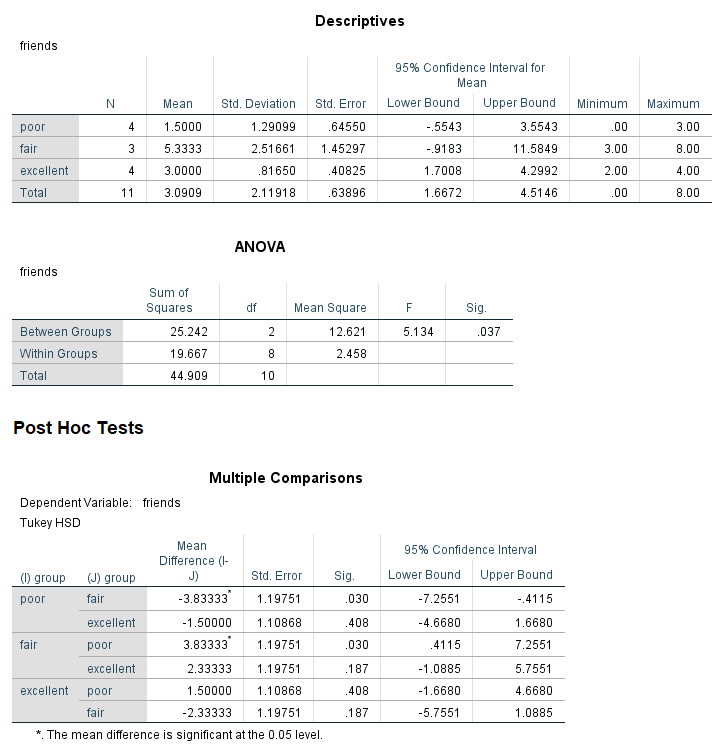
A health psychologist recorded the number of close inter-personal attachments of 45-year-olds who were in excellent, fair, or poor health. People in the Excellent Health group had 4, 3, 2, and 3 close attachments; people in the Fair Health group had 3, 5, and 8 close attachments; and people in the Poor Health group had 3, 1, 0, and 2 close attachments. The data are available on GitHub. Example output from JASP, SPSS, and SAS are shown below.

JASP One-Way ANOVA JASP

SPSS One-Way ANOVA SPSS

SAS One-Way ANOVA SAS

Function in R:

epsilon.full.SS(dfm = 2, dfe = 8, msm = 12.621, mse = 2.458, sst = 44.909, a)

MOTE

Screenshot

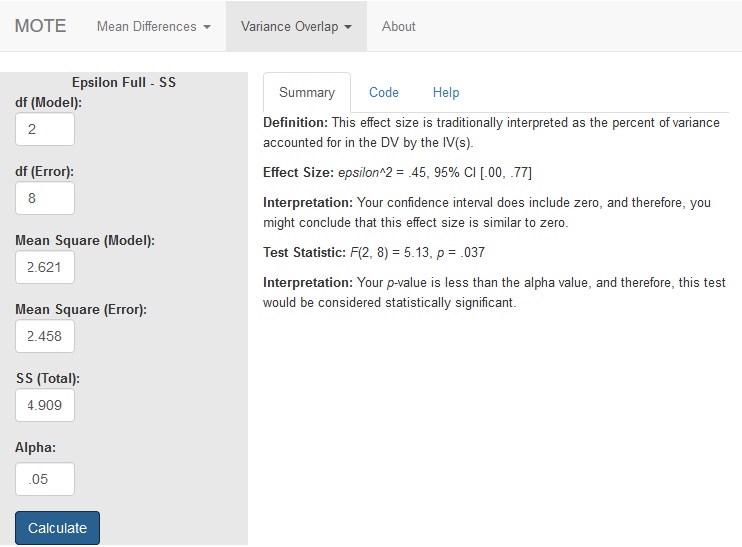
Epsilon for ANOVA Screenshot

Effect Size:

$\epsilon\^2$ = .45, 95% CI [.00, .77]

Interpretation:

Your confidence interval does include zero, and therefore, you might conclude that this effect is similar to zero.

Summary Statistics:

F(2, 8) = 5.13, p = .037

Test Statistic:

Not applicable.

Interpretation:

Your p-value is less than the alpha value, and therefore, this test would be considered statistically significant.

Tutorial