Description

This function displays $d_{\Delta}$ for between subjects data and the non-central confidence interval using the control group standard deviation as the denominator.

The formula for $d_{\Delta}$ is $$d_{\Delta} = {M_{control} - M_{exp}\over SD_{control}}$$

The formula for t is $$t = {M_{control} - M_{exp}\over SE_{pooled}}$$

R Function

delta.ind.t(m1, m2, sd1, sd2, n1, n2, a = 0.05)

Arguments

• m1 = mean from control group
• m2 = mean from experimental group
• sd1 = standard deviation from control group
• sd2 = standard deviation from experimental group
• n1 = sample size from control group
• n2 = sample size from experimental group
• a = significance level

Example

A forensic psychologist conducted a study to examine whether being hypnotized during recall affects how well a witness can remember facts about an event. Eight participants watched a short film of a mock robbery, after which each participant was questioned about what he or she had seen. The four participants in the experimental group were questioned while they were hypnotized and gave 14, 22, 18, and 17 accurate responses. The four participants in the control group gave 20, 25, 24, and 23 accurate responses. The data are available on GitHub. Example output from JASP, SPSS, and SAS are shown below.

JASP

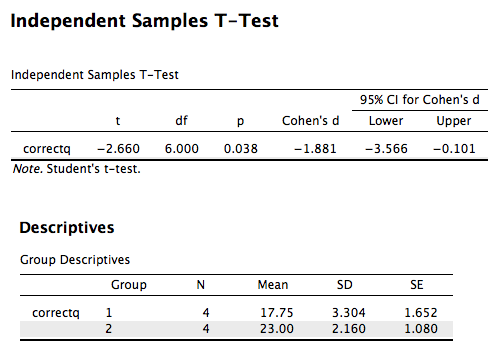
SPSS

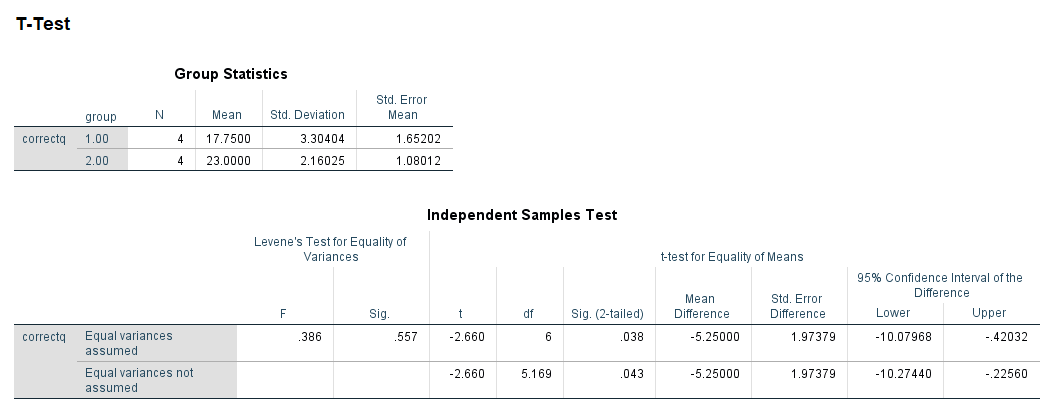
SAS

Function in R:

delta.ind.t(m1 = 17.75, m2 = 23.00, sd1 = 3.304, sd2 = 2.160, n1 = 4, n2 = 4, a = .05)

MOTE

Screenshot

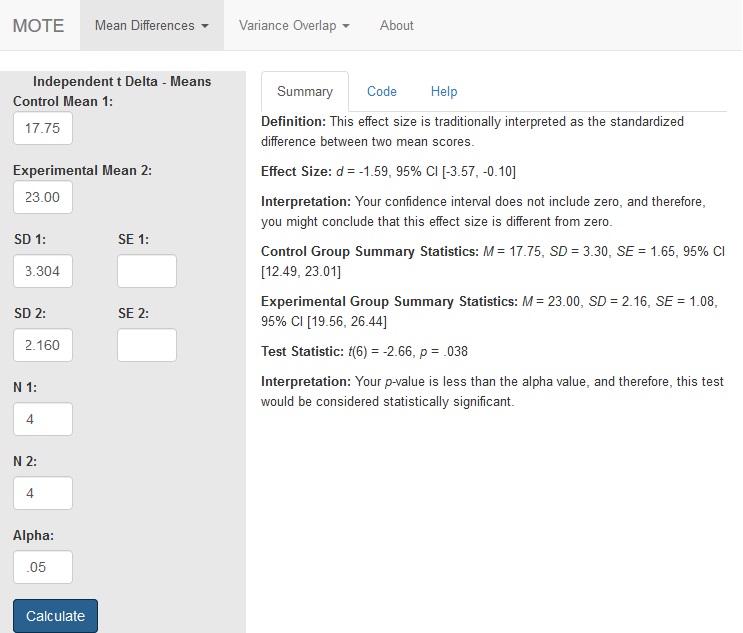
Effect Size:

$d_{\Delta}$ = -1.59, 95% CI [-3.57, -0.10]

Interpretation:

Your confidence interval does not include zero, and therefore, you might conclude that this effect size is different from zero.

Summary Statistics:

Control Group Summary Statistics: M = 17.75, SD = 3.30, SE = 1.65, 95% CI [12.49, 23.01]

Experimental Group Summary Statistics: M = 23.00, SD = 2.16, SE = 1.08, 95% CI [19.56, 26.44]

Test Statistic:

t(6) = -2.66, p = .038

Interpretation:

Your p-value is less than the alpha value, and therefore, this test would be considered statistically significant.

Tutorial