Description

The formula for $\eta^2$ is: $$\frac{SS_{model}} {SS_{total}}$$

R Function

eta.full.SS(dfm, dfe, ssm, sst, Fvalue, a)

Arguments

• dfm = degrees of freedom for the model/IV/between
  
• dfe = degrees of freedom for the error/residual/within
• ssm = sum of squares for the model/IV/between
• sst = sum of squares total
• Fvalue = F statistic
  
• a = significance level

Example

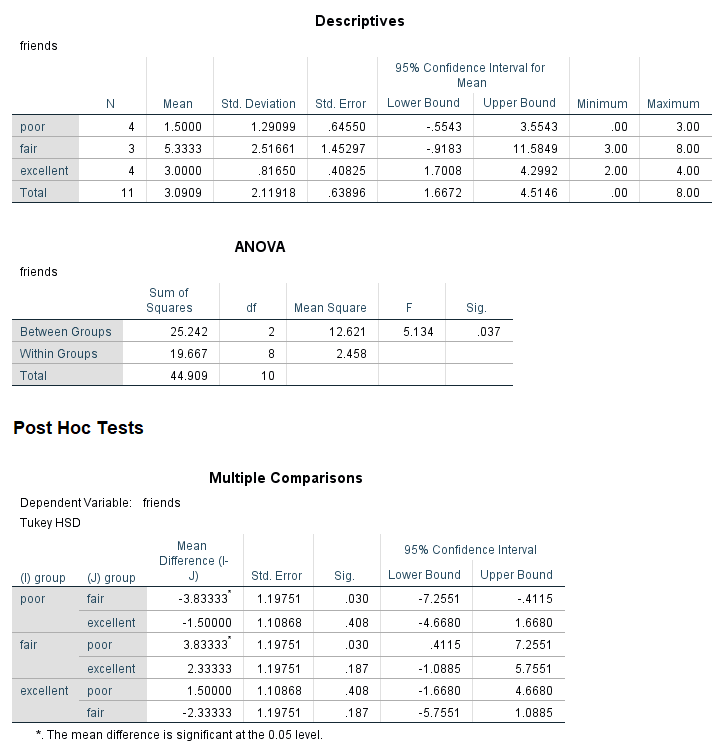
A health psychologist recorded the number of close inter-personal attachments of 45-year-olds who were in excellent, fair, or poor health. People in the Excellent Health group had 4, 3, 2, and 3 close attachments; people in the Fair Health group had 3, 5, and 8 close attachments; and people in the Poor Health group had 3, 1, 0, and 2 close attachments. The data are available on GitHub. Example output from JASP, SPSS, and SAS are shown below.

JASP

SPSS

SAS

• dfm = 2
  
• dfe = 8
• ssm = 25.24
• sst = 44.91
• Fvalue = 5.13
  
• a = .05

Function in R:

eta.full.SS(dfm = 2, dfe = 8, ssm = 25.24, sst = 44.91, Fvalue = 5.13, a = 0.05)

MOTE

Screenshot

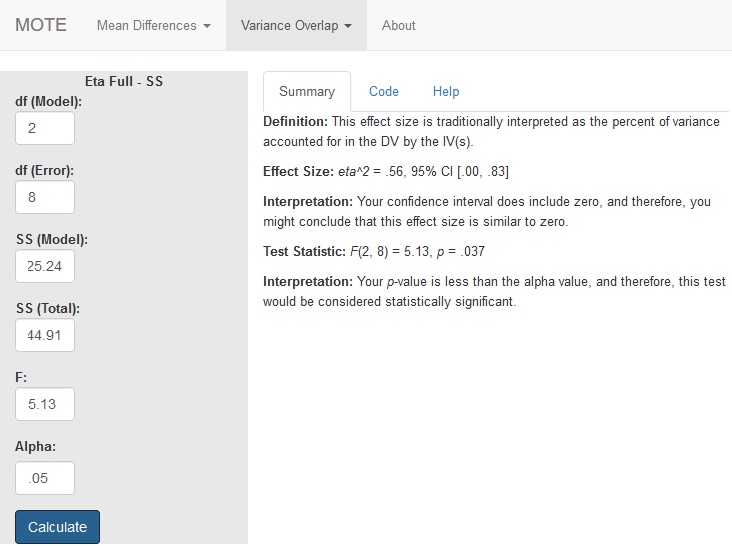
Effect Size:

$\eta^2$ = .56, 95% CI [.00, .83]

Interpretation:

Your confidence interval does include zero, and therefore, you might conclude that this effect size is similar to zero.

Summary Statistics:

Not applicable.

Test Statistic:

F(2, 8) = 5.13, p = .037

Interpretation:

Your p-value is less than the alpha value, and therefore, this test would be considered statistically significant.

Tutorial