Description

This function displays d and central confidence interval calculated from differences in independent proportions.

The formula for d is: $$d = \frac{P_1}{SE_1} - \frac{P_2}{SE_2}$$

The formula for Z is: $$Z = \frac{P_1 - P_2}{SE}$$

R Function

d.prop(p1, p2, n1, n2, a)

Arguments

• p1 = proportion of people group one
• p2 = proportion of people group two
• n1 = sample size group one
• n2 = sample size group two
• a = significance level

Example

Several researchers were examining the data on the number of students who retake a course after they receive a D, F, or withdraw from the course. They randomly sampled form a large university two groups of students: traditional (less than 25 years old) and non-traditional (25 and older). Each group included 100 participants. The traditional group showed about 25% of students who would retake a course, while the non-traditional group showed about 35% would retake the course.

Function in R:

d.prop(p1 = .25, p2 = .35, n1 = 100, n2 = 100, a = .05)

MOTE

Screenshot

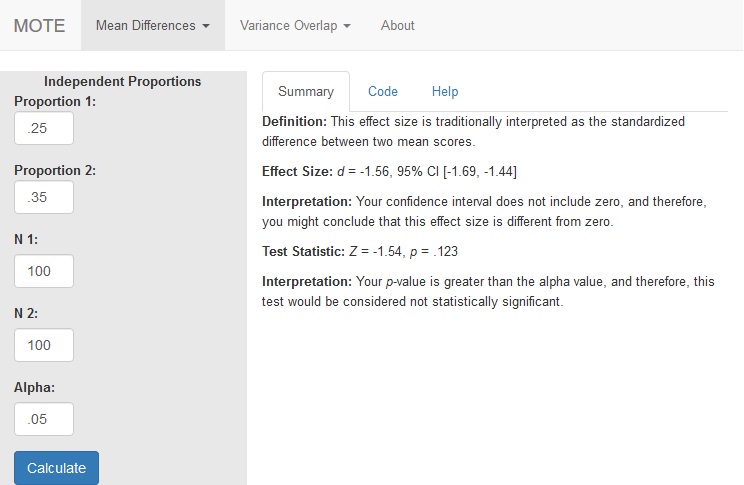
Effect Size:

d = -1.56, 95% CI [-1.69, -1.44]

Interpretation:

Your confidence interval does not include zero, and therefore, you might conclude that this effect size is different from zero.

Summary Statistics:

Not applicable.

Test Statistic:

Z = -1.54, p = .123

Interpretation:

Your p-value is greater than the alpha value, and therefore, this test would be considered not statistically significant.

Tutorial