Description

This function displays omega squared from ANOVA analyses and its non-central confidence interval based on the F distribution. This formula is appropriate for multi-way between subjects designs.

The formula for $\omega_p^2$ is: $$\frac{df_{model} \times (MS_{model} - MS_{error})}{SS_{model} + (N - df_{model}) \times MS_{error}}$$

The formula for F is: $$\frac{MS_{model}}{MS_{error}}$$

R Function

omega.partial.SS.bn(dfm, dfe, msm, mse, ssm, n, a)

Arguments

  • dfm = degrees of freedom for the model/IV/between
  • dfe = degrees of freedom for the error/residual/within
  • msm = mean square for the model/IV/between
  • mse = mean square for the error/residual/within
  • ssm = sum of squares for the model/IV/between
  • n = total sample size
  • a = significance level

Example

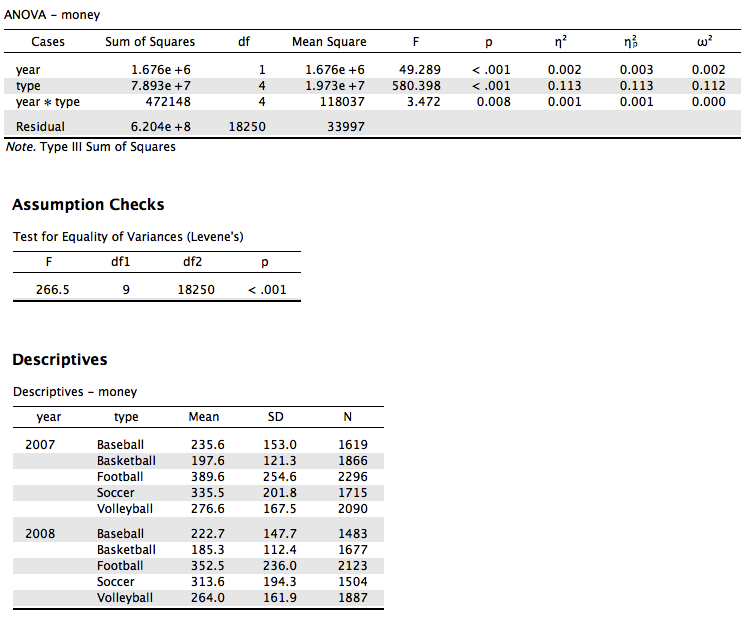
We looked at two year’s worth of athletic spending data (treating each receipt and years as separate between subjects’ events) for four different sports. Are there differences across sports and years in spending?

JASP Two Way ANOVA Between-Subjects JASP

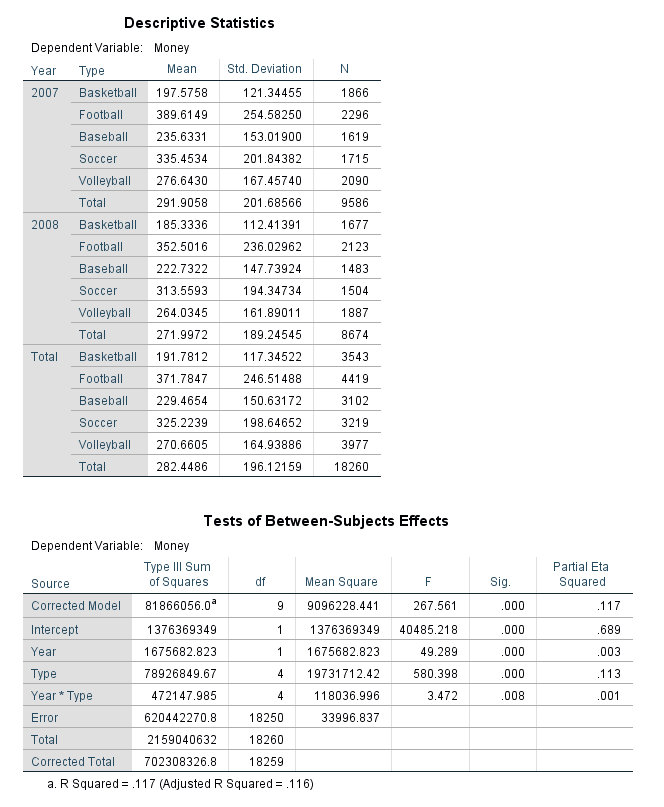
SPSS Two-Way Between-Subjects SPSS

SAS Two-Way Between-Subjects ANOVA SAS

Function in R:

omega.partial.SS.bn(dfm = 1, dfe = 18250, msm = 1675682.823, mse = 33996.837, ssm = 1675682.823, n = 18260, a = 0.05)

MOTE

Screenshot

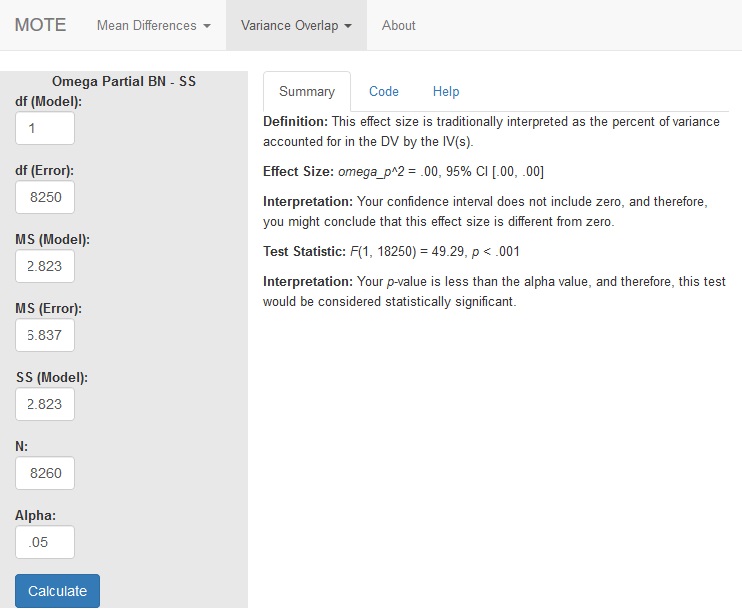
Omega Partial SS Screenshot

Effect Size:

$\omega_p^2$ = .00, 95% CI [.00, .00]

Interpretation:

Your confidence interval does not include zero, and therefore, you might conclude that this effect size is different from zero.

Summary Statistics:

Not applicable.

Test Statistic:

F(1, 18250) = 49.29, p < .001

Interpretation:

Your p-value is less than the alpha value, and therefore, this test would be considered statistically significant.

Tutorial