Description

This function displays d and non-central confidence interval for d for single t tests from means.

The formula for d is: $$d = \frac{M - \mu}{SD}$$

The formula for t is: $$t = \frac{M - \mu}{SE}$$

R Function

d.single.t(m, u, sd, n, a = 0.05)

Arguments

  • m = sample mean
  • u = population mean
  • sd = sample standard deviation
  • n = sample size
  • a = significance level

Example

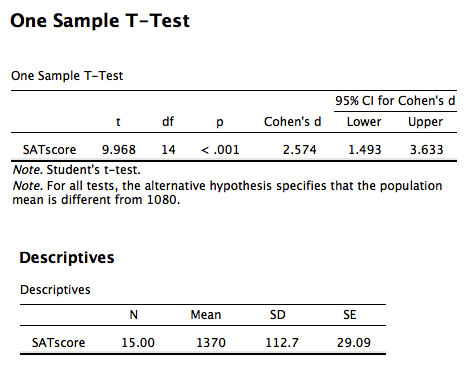
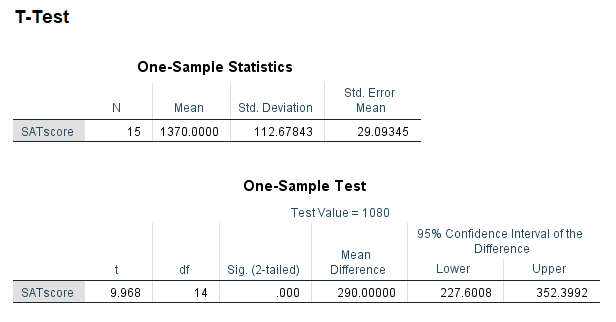
A school has a gifted/honors program that they claim is significantly better than others in the country. The gifted/honors students in this school scored an average of 1370 on the SAT, while the national average for gifted programs is a SAT score of 1080. The data are available on GitHub. Example output from JASP, SPSS, and SAS are shown below.

JASP Single t JASP

SPSS Single t SPSS

SAS Single t SAS

Function in R:

d.single.t(m = 1370, u = 1080, sd = 112.7, n = 15, a = .05)

MOTE

Screenshot

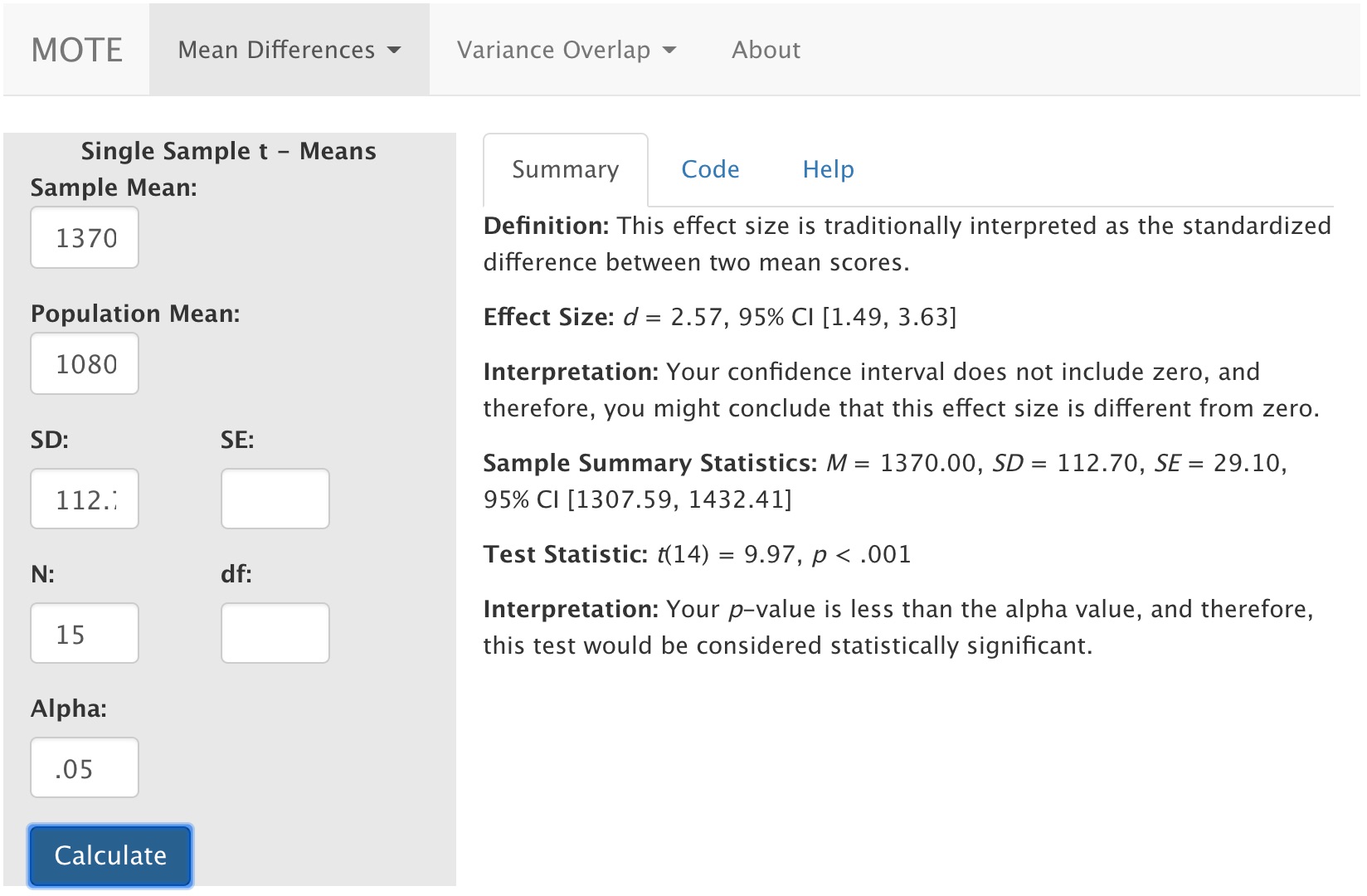
Single-Sample t - Means Screenshot

Effect Size:

Effect Size: d = 2.57, 95% CI [1.49, 3.63]

Interpretation:

Your confidence interval does not include zero, and therefore, you might conclude that this effect size is different from zero.

Summary Statistics:

M = 1370.00, *S*D = 112.70, *S*E = 29.10, 95% CI [1307.59, 1432.41]

Test Statistic:

t(14) = 9.97, p < .001

Interpretation:

Your p-value is less than the alpha value, and therefore, this test would be considered statistically significant.

Tutorial