Description

The formula for $\eta_G^2$ is: $$\frac{SS_{model}}{SS_{model} + SS_{subject} + SS_{error}}$$

R Function

ges.partial.SS.mix(dfm, dfe, ssm, sss, sse, Fvalue, a = 0.05)

Arguments

  • dfm = degrees of freedom for the model/IV/between
  • dfe = degrees of freedom for the error/residual/within
  • ssm = sum of squares for the model/IV/between
  • sss = sum of squares subject variance
  • sse = sum of squares for the error/residual/within
  • Fvalue = F statistic
  • a = significance level

Example

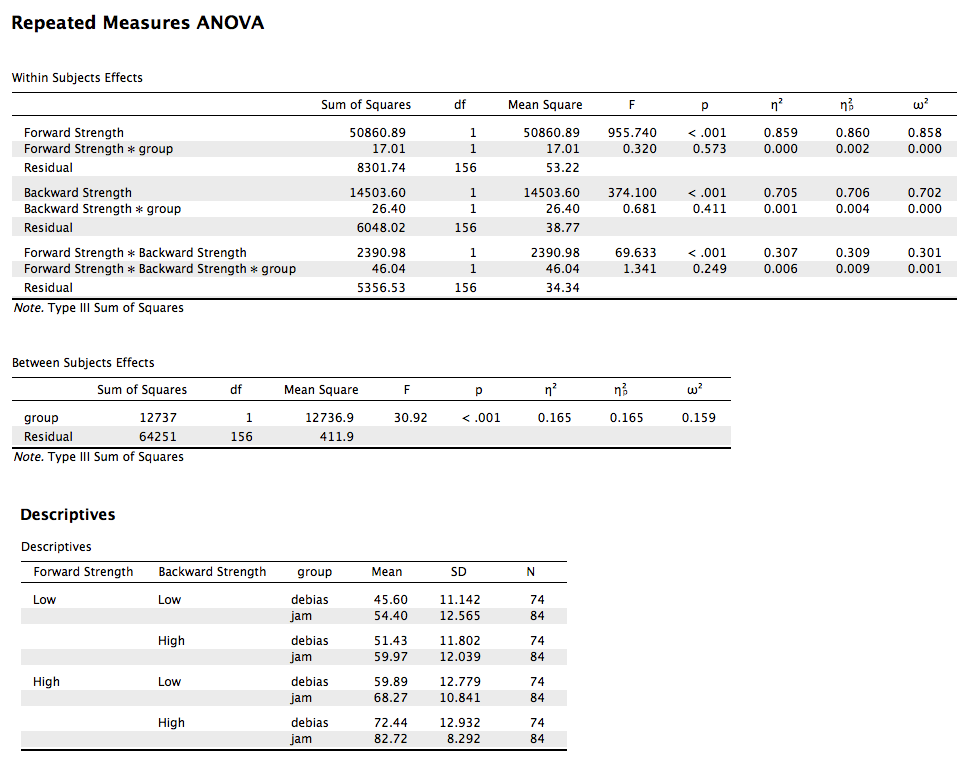
Given previous research, we know that backward strength in free association tends to increase the ratings participants give when you ask them how many people out of 100 would say a word in response to a target word (like Family Feud). This result is tied to people’s overestimation of how well they think they know something, which is bad for studying. So, we gave people instructions on how to ignore the BSG. Did it help? Is there an interaction between BSG and instructions given? The data are available on GitHub. Example output from JASP, SPSS, and SAS are shown below.

JASP Two Way Mixed ANOVA JASP

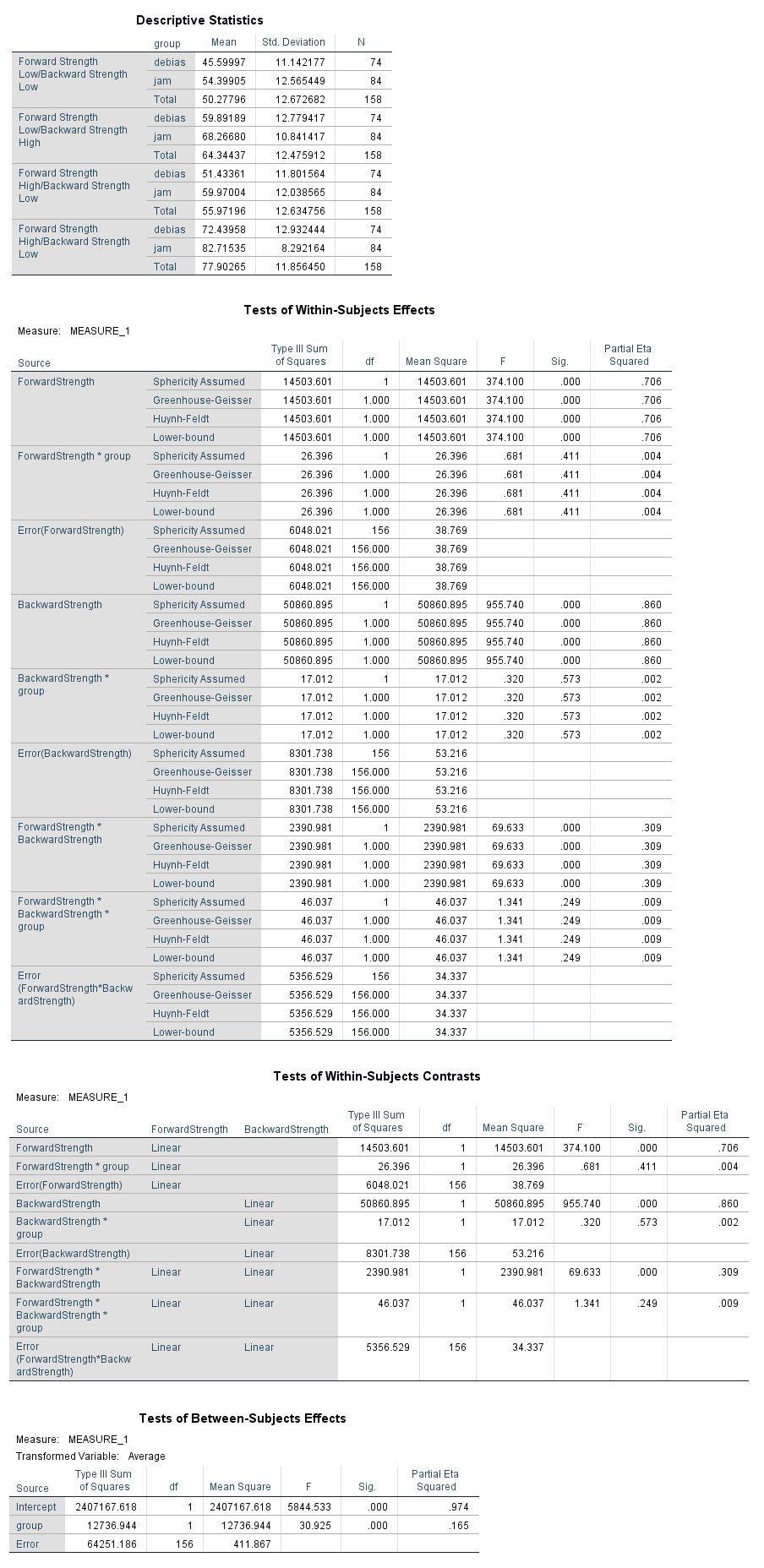
SPSS Two Way Mixed ANOVA SPSS

SAS Two Way Mixed ANOVA SAS

Function in R:

ges.partial.SS.mix(dfm = 1, dfe = 156, ssm = 50860.89, sss = 64251, sse = 8301.74, Fvalue = 955.740, a = .05)

MOTE

Screenshot

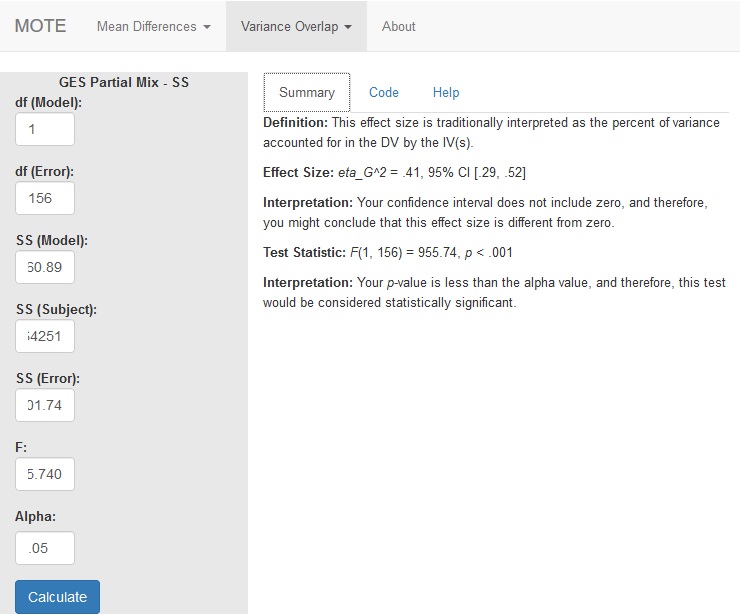
GES Partial Mixed SS Screenshot

Effect Size:

$\eta_G^2$ = .41, 95% CI [.29, .52]

Interpretation:

Your confidence interval does not include zero, and therefore, you might conclude that this effect size is different from zero.

Summary Statistics:

Not applicable.

Test Statistic:

F(1, 156) = 955.74, p < .001

Interpretation:

Your p-value is less than the alpha value, and therefore, this test would be considered statistically significant.

Tutorial