Description

The formula for $\omega_p^2$ is: $$\frac{df_{model} \times (MS_{model} - MS_{error})}{SS_{model} + (N - df_{model}) \times MS_{error}}$$

The formula for F is: $$\frac{MS_{model}}{MS_{error}}$$

R Function

omega.partial.SS.rm(dfm, dfe, msm, mse, ssm, sse, sss, a)

Arguments

• dfm = degrees of freedom for the model/IV/between
  
• dfe = degrees of freedom for the error/residual/within
• msm = mean square for the model/IV/between
• mse = mean square for the error/residual/within
• mss = mean square for the subject variance
• ssm = sum of squares for the model/IV/between
• sse = sum of squares for the error/residual/within
• sss = sum of squares subject variance
• a = significance level

Example

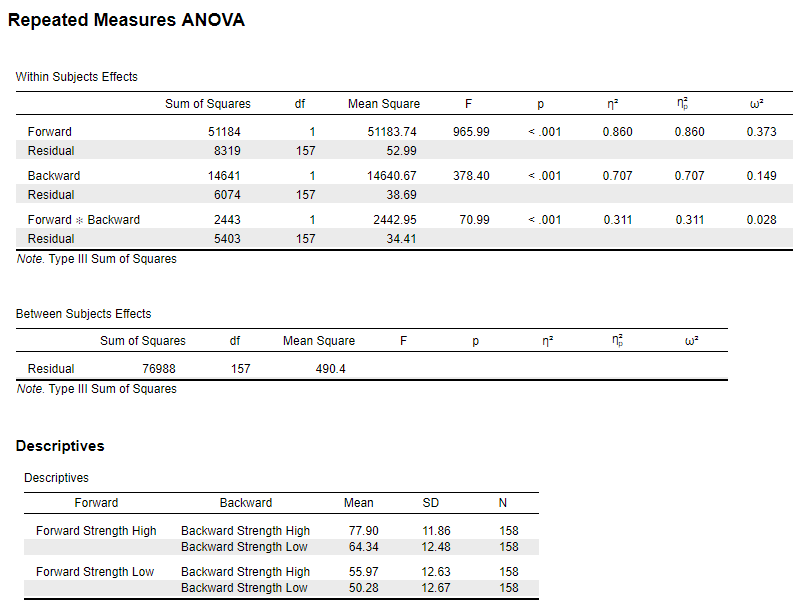
In this experiment people were given word pairs to rate based on their “relatedness”. How many people out of a 100 would put LOST-FOUND together? Participants were given pairs of words and asked to rate them on how often they thought 100 people would give the second word if shown the first word. The strength of the word pairs was manipulated through the actual rating (forward strength: FSG) and the strength of the reverse rating (backward strength: BSG). Is there an interaction between FSG and BSG when participants are estimating the relation between word pairs? The data are available on GitHub. Example output from JASP, SPSS, and SAS are shown below.

JASP

SPSS

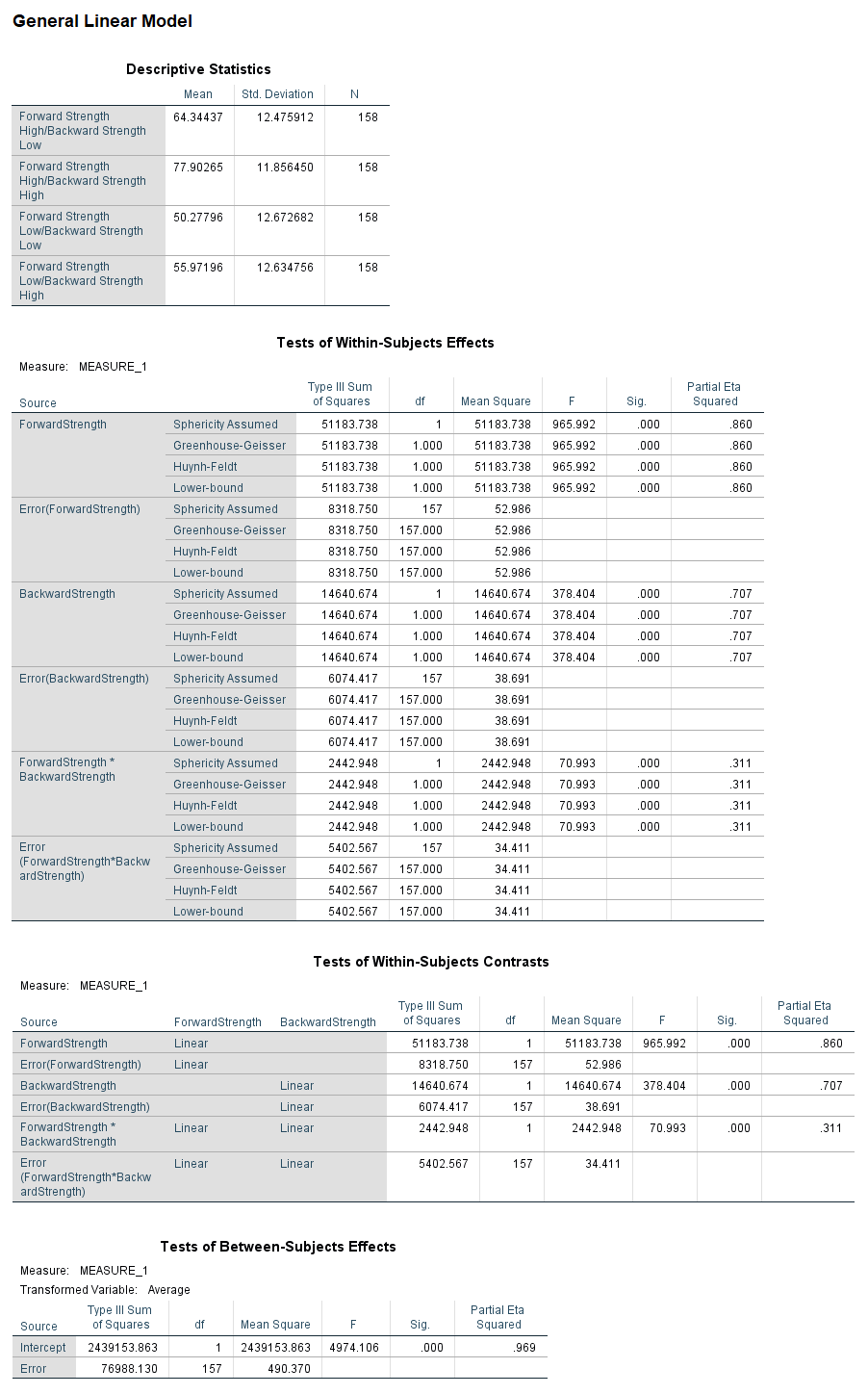
SAS

Function in R:

omega.partial.SS.rm(dfm = 1, dfe = 156, msm = 4995, mse = 35.52, mss = 493, ssm = 4995, sse = 5541, sss = 76908, a = .05)

MOTE

Screenshot

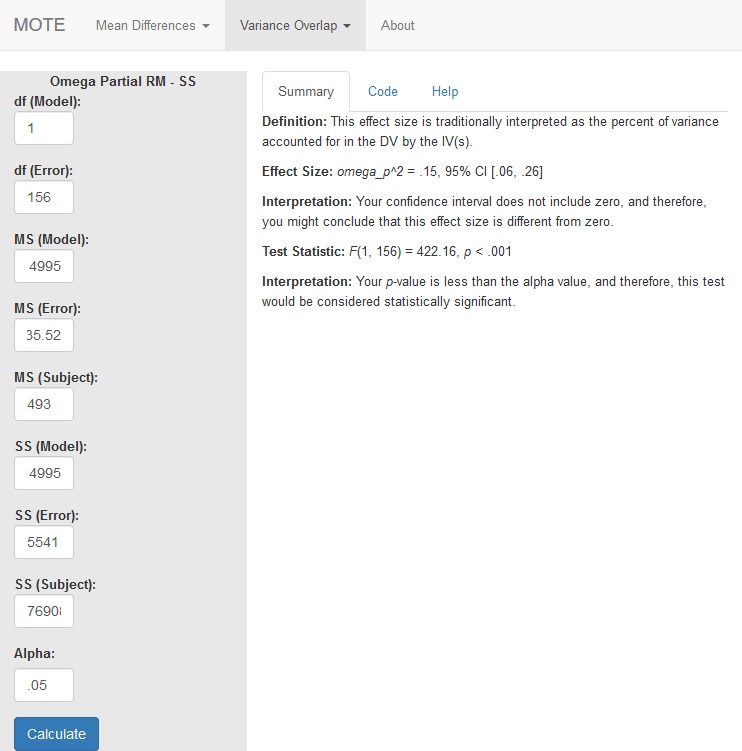
Effect Size:

$\omega_p^2$ = .15, 95% CI [.06, .26]

Interpretation:

Your confidence interval does not include zero, and therefore, you might conclude that this effect size is different from zero.

Summary Statistics:

Not applicable.

Test Statistic:

F(1, 156) = 422.16, p < .001

Interpretation:

Your p-value is less than the alpha value, and therefore, this test would be considered statistically significant.

Tutorial