Chi-Square Odds Ratios
Description
This function displays odds ratios and their normal confidence intervals. This statistic is calculated as (level 1.1/level 1.2) / (level 2.1/level 2.2), which can be considered the odds of level 1.1 given level1 overall versus level2.1 given level2 overall.
The formula for odds is: $$\frac{(N_{11}/N_{12})}{(N_{21}/N_{22})}$$
R Function
odds(n11, n12, n21, n22, a)
Arguments
- n11 = sample size for level 1.1
- n12 = sample size for level 1.2
- n21 = sample size for level 2.1
- n22 = sample size for level 2.2
- a = significance level
Example
A health psychologist was interested in the rates of anxiety in first generation and regular college students. They polled campus and found the following data:
| First Generation | Regular | |
|---|---|---|
| Low Anxiety | 10 | 50 |
| High Anxiety | 20 | 15 |
Function in R:
odds(n11 = 10, n12 = 50, n21 = 20, n22 = 15, a = 0.05)
MOTE
Screenshot
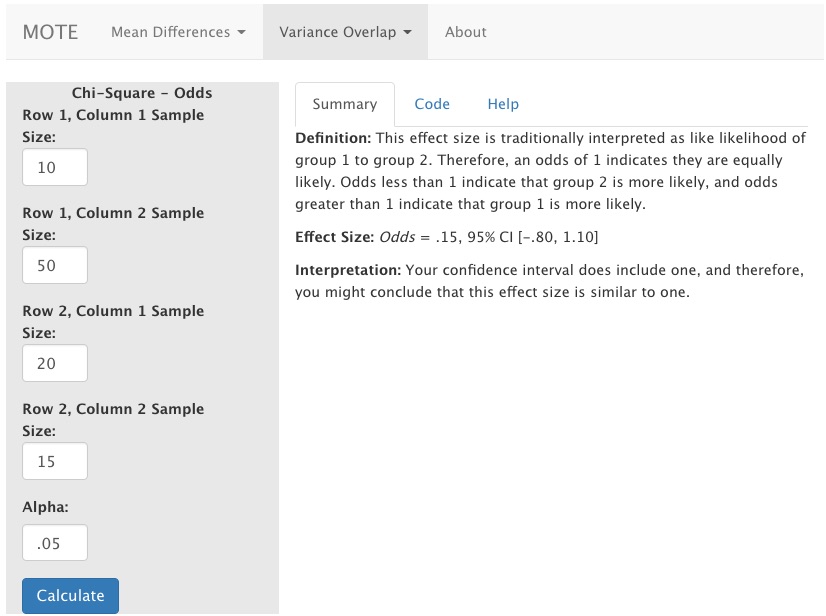
Effect Size:
This effect size is traditionally interpreted as like likelihood of group 1 to group 2. Therefore, an odds of 1 indicates they are equally likely. Odds less than 1 indicate that group 2 is more likely, and odds greater than 1 indicate that group 1 is more likely.
Odds = .15, 95% CI [-.80, 1.10]
Interpretation:
Your confidence interval does not include one, and therefore, you might conclude that this effect size is different from one.
Summary Statistics:
Not applicable.
Test Statistic:
Not applicable.
Interpretation:
Not applicable.
