Description

This function displays V and non-central confidence interval for the specified chi-square statistic.

The formula for V is: $$\sqrt{ \frac{\chi^2} {N \times df_{smaller}} } $$

$df_{smaller}$ is defined by the minimum of (rows - 1) or (columns - 1).

R Function

v.chi.sq(x2, n, r, c, a = 0.05)

Arguments

  • x2 = chi-square statistic
  • n = sample size
  • r = number of rows in the contingency table
  • c = number of columns in the contingency table
  • a = significance level

Example

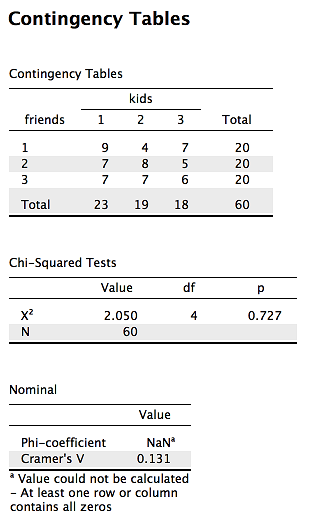
Individuals were polled about their number of friends (low, medium, high) and their number of kids (1, 2, 3+) to determine if there was a relationship between friend groups and number of children, as we might expect that those with more children may have less time for friendship maintaining activities. The data are available on GitHub. Example output from JASP, SPSS, and SAS are shown below.

JASP Chi-square JASP

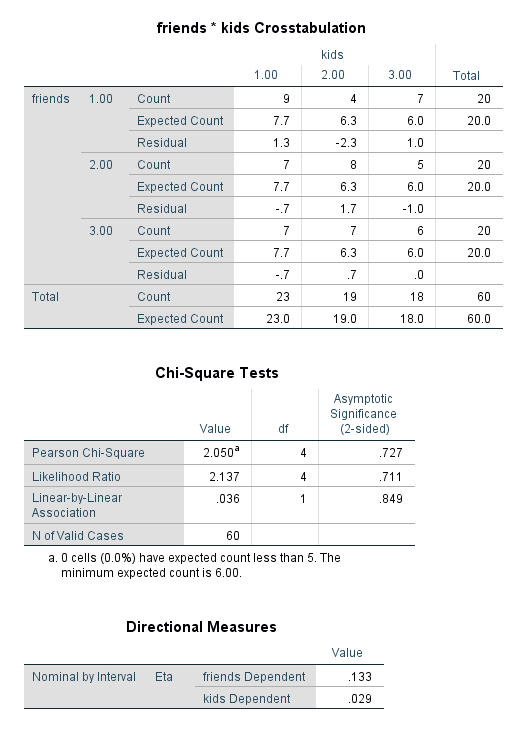
SPSS Chi-square SPSS

SAS Chi-square SAS

Function in R:

v.chi.sq(x2 = 2.05, n = 60, r = 3, c = 3, a = 0.05)

MOTE

Screenshot

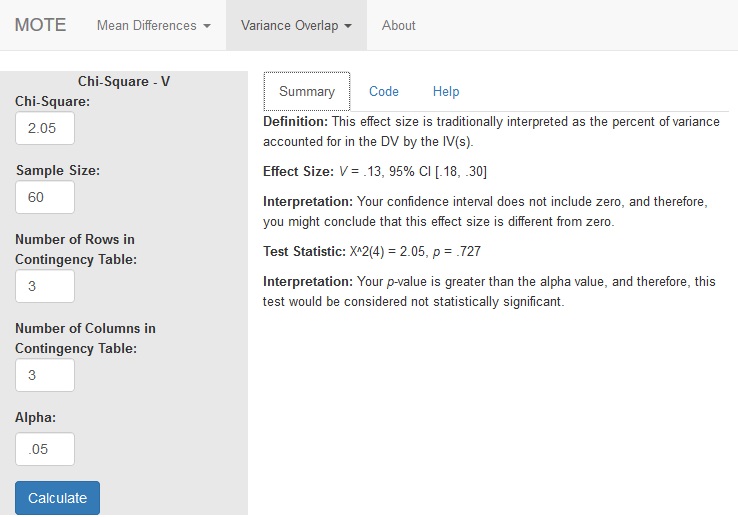
Chi-Square V Screenshot

Effect Size:

This effect size is traditionally interpreted as the percent of variance accounted for in the DV by the IV(s).

V = .13, 95% CI [.18, .30]

Interpretation:

Your confidence interval does not include zero, and therefore, you might conclude that this effect size is different from zero.

Summary Statistics:

Not applicable.

Test Statistic:

$\chi^2(4)$ = 2.05, p = .727

Interpretation:

Your p-value is greater than the alpha value, and therefore, this test would be considered not statistically significant.

Tutorial