Description

The formula for $\eta_G^2$ is: $$\frac{SS_{model}}{SS_{model} + SS_{subject} + SS_{errorA} + SS_{errorB} + SS_{errorAxB}}$$

The labels A and B here indicate the two IVs in a two-way design. AxB indicates the interaction term for A by B. This formula does not cover more than two-way designs.

R Function

ges.partial.SS.rm(dfm, dfe, ssm, sss, sse1, sse2, sse3, Fvalue, a)

Arguments

  • dfm = degrees of freedom for the model/IV/between
  • dfe = degrees of freedom for the error/residual/within
  • ssm = sum of squares subject variance
  • sse1 = sum of squares for the error/residual/within for the first IV
  • sse2 = sum of squares for the error/residual/within for the second IV
  • sse3 = sum of squares for the error/residual/within for the interaction
  • Fvalue = F statistic
  • a = significance level

Example

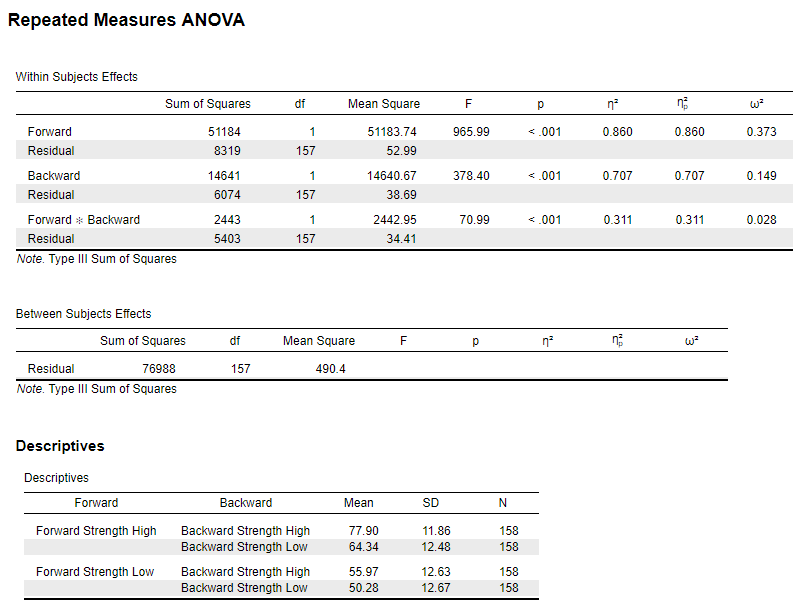
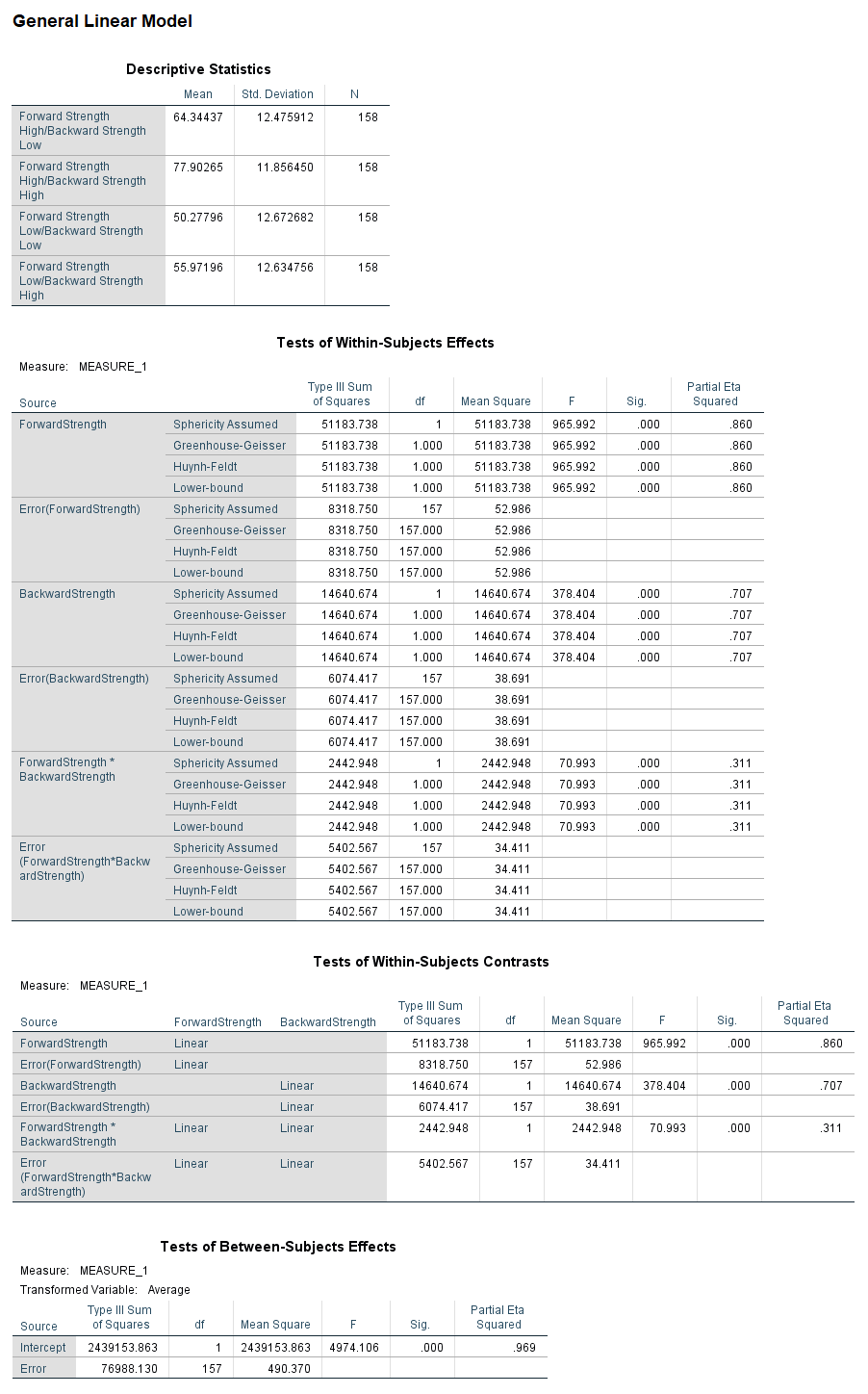
In this experiment people were given word pairs to rate based on their “relatedness”. How many people out of a 100 would put LOST-FOUND together? Participants were given pairs of words and asked to rate them on how often they thought 100 people would give the second word if shown the first word. The strength of the word pairs was manipulated through the actual rating (forward strength: FSG) and the strength of the reverse rating (backward strength: BSG). Is there an interaction between FSG and BSG when participants are estimating the relation between word pairs? The data are available on GitHub. Example output from JASP, SPSS, and SAS are shown below.

JASP Repeated Measures Two-Way ANOVA JASP

SPSS Repeated Measures Two-Way ANOVA SPSS

SAS Repeated Measures Two-Way ANOVA SAS

Function in R:

ges.partial.SS.rm(dfm = 1, dfe = 157, ssm = 51184, sss = 76988, sse1 = 8319, sse2 = 6074, sse3 = 5403, Fvalue = 5.46, a = .05)

MOTE

Screenshot

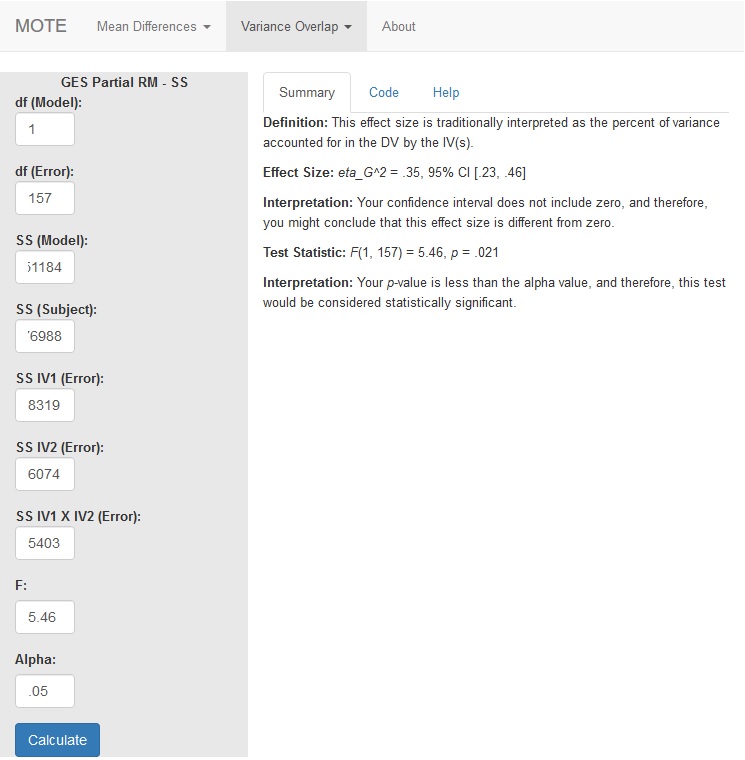
Repeated Measures Two-Way ANOVA Screenshot

Effect Size:

$\eta_{G}^2$ = .35, 95% CI [.23, .46]

Interpretation:

Your confidence interval does not include zero, and therefore, you might conclude that this effect size is different from zero.

Summary Statistics:

Not applicable.

Test Statistic:

F(1, 157) = 5.46, p = .021

Interpretation:

Your p-value is less than the alpha value, and therefore, this test would be considered statistically significant.

Tutorial