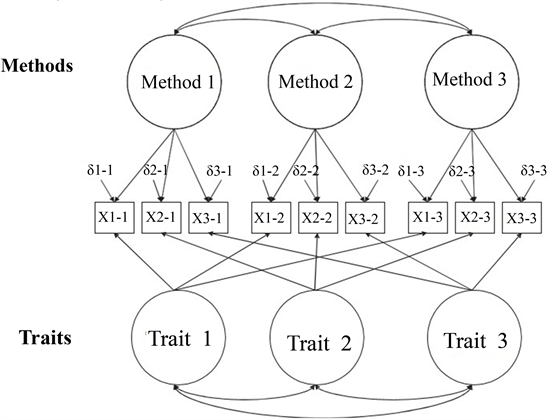
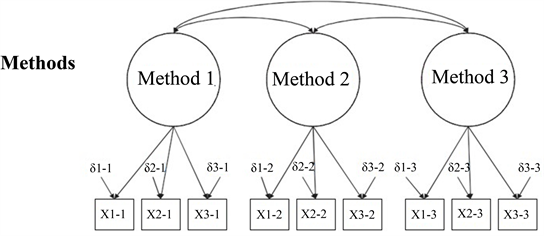
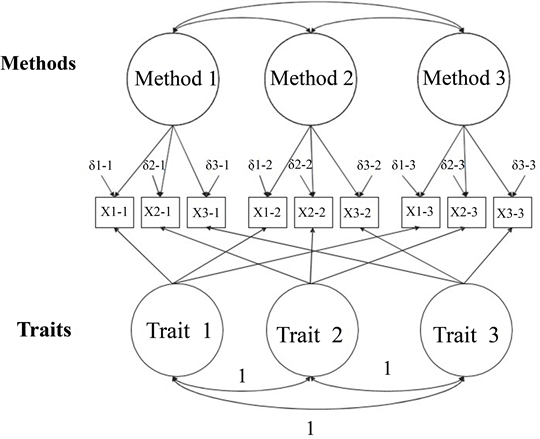
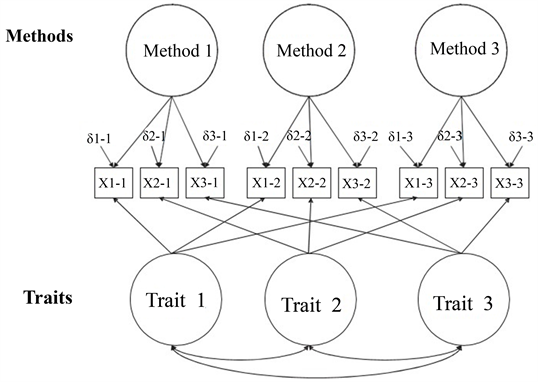
Multi-Trait Multi-Method • learnSEM

Multi-Trait Multi-Method SEM

Another good resource includes: http://davidakenny.net/cm/mtmm.htm
Traits: the latent factors you are trying to measure.
Methods: the way you are measuring the latent factors.

When to Use

Convergent validity: How much do different assessments measure the same traits?
- We would like measurement 1 and measurement 2 to assess the trait equally well.
Discriminant validity: How much do different assessment methods diverge in measurement of different traits?
- We would like measurement 1 and measurement 2 to assess each trait differently.
Both of these together would indicate that each measurement is equally useful.

When to Use

Method effects: How much do the measurements cause overlap in traits?
- We want measurement 1 to measure trait 1 and trait 2 differently.

Logic of MTMM

We will build several different models that test the questions listed above and compare them using nested χ2\chi^2 tests using the anova() function.
- We could also use AIC or ECVI, but generally the chi-square test is preferred.
Another popular model comparison rule is the $\Delta$ CFI > .01 would be considered a significant change in fit.

The Steps

There are two approaches to MTMM
- Widaman (1985) approach
- Correlated uniqueness approach

The Steps

Let’s note that our model specification is slightly different than a normal CFA.
We will not use the normal scaling on the manifest variables.
We will instead set the variance to each latent to one using std.lv = TRUE.

Model 1: Correlated Traits / Correlated Methods

You will correlate traits with each other.
You will correlate methods with each other.
You will NOT cross correlate methods and traits.
So how can we force lavaan to do that?
- latent ~~ 0*latent

Model 1: Correlated Traits / Correlated Methods

One of the big concerns/complaints with the traditional MTMM steps is that Model 1 is likely to create a Heywood case with a negative error variance.
Generally, because these models are complex … most of the latent variables are correlated on purpose, so it may be hard to estimate.

Model 1: Correlated Traits / Correlated Methods

If you get a Heywood case of negative variance:
- If you know the variance by having the real data, set it to that.
- Set the value to something small and positive.
- Set the value equal to another small positive parameter.

Model 1: Correlated Traits / Correlated Methods

All other models are compared to Model 1.
Model 1 represents the best case scenario, wherein traits are correlated but not perfectly and they are estimated by the measurements but not perfectly.

Example Data

Traits:
- Meaning: MLQ 1, 2, 5, 10 and PIL 4, 12, 17
- Purpose: MLQ 3, 4, 6, 8, 9, and PIL 3, 8, 20
Methods:
- Purpose in Life Test (p questions)
- Meaning in Life Questionnaire (m questions)

library(lavaan)
library(semPlot)
library(rio)

meaning.data <- import("data/lecture_mtmm.csv")
str(meaning.data)
#> 'data.frame':    567 obs. of  70 variables:
#>  $ p1 : int  5 1 6 5 5 4 5 6 6 6 ...
#>  $ p2 : num  5 3 6 5 6 5 6 6 6 5 ...
#>  $ p3 : int  7 5 7 5 5 6 6 7 5 7 ...
#>  $ p4 : int  7 5 6 6 7 7 7 7 5 5 ...
#>  $ p5 : int  4 2 7 3 6 4 6 5 4 6 ...
#>  $ p6 : int  5 5 7 5 6 4 5 6 3 6 ...
#>  $ p7 : num  7 5 7 6 5 6 7 7 5 7 ...
#>  $ p8 : int  5 5 6 5 5 5 5 6 5 7 ...
#>  $ p9 : int  7 3 6 5 7 5 6 7 4 6 ...
#>  $ p10: int  6 3 7 6 7 5 6 6 3 4 ...
#>  $ p11: int  7 4 6 6 7 7 6 7 4 6 ...
#>  $ p12: int  4 5 7 5 1 5 6 5 4 5 ...
#>  $ p13: num  7 5 6 6 6 5 7 4 6 7 ...
#>  $ p14: num  4 7 6 5 6 5 7 7 7 1 ...
#>  $ p15: num  7 5 6 5 7 3 6 3 2 5 ...
#>  $ p16: int  7 7 7 5 7 7 6 7 2 6 ...
#>  $ p17: num  5 5 5 6 7 5 6 7 5 5 ...
#>  $ p18: int  1 7 7 6 7 5 1 1 6 5 ...
#>  $ p19: int  5 3 6 5 6 4 5 6 4 6 ...
#>  $ p20: int  6 5 7 5 5 6 6 7 4 5 ...
#>  $ l1 : num  1 0 1 1 1 1 1 1 1 1 ...
#>  $ l2 : int  1 0 1 1 1 1 1 0 1 1 ...
#>  $ l3 : int  1 1 1 1 1 1 1 1 1 1 ...
#>  $ l4 : num  1 0 1 1 1 1 1 1 1 1 ...
#>  $ l5 : int  0 0 1 0 1 0 1 0 1 1 ...
#>  $ l6 : int  1 0 1 1 1 1 0 1 0 1 ...
#>  $ l7 : num  1 1 1 1 1 1 1 1 1 1 ...
#>  $ l8 : int  1 1 1 1 0 0 0 1 1 1 ...
#>  $ l9 : int  1 0 1 1 1 1 1 1 1 1 ...
#>  $ l10: num  1 0 1 0.77 1 1 0 1 0 0 ...
#>  $ l11: int  1 0 1 1 1 1 1 1 0 1 ...
#>  $ l12: num  1 1 1 1 1 1 1 1 1 1 ...
#>  $ l13: int  1 1 1 1 1 1 1 1 1 1 ...
#>  $ l14: int  0 1 1 1 1 1 1 1 1 0 ...
#>  $ l15: num  1 0 1 0 1 0 0 0 0 0 ...
#>  $ l16: int  1 1 1 1 1 1 1 1 0 1 ...
#>  $ l17: num  1 0 1 1 1 1 1 1 1 1 ...
#>  $ l18: int  0 1 1 0 1 0 1 1 1 1 ...
#>  $ l19: num  0 0 1 1 1 0 1 0 1 1 ...
#>  $ l20: int  1 0 1 1 1 1 1 1 0 1 ...
#>  $ m1 : int  6 4 6 6 7 5 7 6 5 5 ...
#>  $ m2 : int  5 7 4 5 3 7 4 5 6 2 ...
#>  $ m3 : int  2 7 3 6 2 6 5 5 6 5 ...
#>  $ m4 : int  4 3 5 6 7 5 4 6 4 5 ...
#>  $ m5 : int  6 4 6 6 7 6 6 7 4 6 ...
#>  $ m6 : int  4 1 6 5 7 6 3 7 3 5 ...
#>  $ m7 : int  2 6 2 5 3 4 4 5 6 2 ...
#>  $ m8 : int  4 3 3 5 2 6 6 4 6 5 ...
#>  $ m9 : int  7 6 7 6 7 6 7 7 5 3 ...
#>  $ m10: int  4 3 1 6 2 4 7 1 5 3 ...
#>  $ s1 : num  2 3 5 3 5 4 4 7 4 1 ...
#>  $ s2 : num  2 3 5 3 5 4 4 6 4 1 ...
#>  $ s3 : num  1 5 2 3 3 2 2 5 5 2 ...
#>  $ s4 : num  1 3 2 2 2 4 3 2 5 2 ...
#>  $ s5 : num  2 5 3 3 1 4 6 4 5 5 ...
#>  $ s6 : num  3 7 6 4 6 6 7 7 7 6 ...
#>  $ s7 : int  5 7 7 4 4 6 7 5 6 6 ...
#>  $ s8 : num  1 7 2 3 1 2 2 6 7 6 ...
#>  $ s9 : num  1 7 2 3 2 2 2 1 2 2 ...
#>  $ s10: num  2 7 4 4 5 2 6 5 5 5 ...
#>  $ s11: num  1 2 2 3 2 2 2 1 4 3 ...
#>  $ s12: num  1 7 2 3 2 2 3 3 2 4 ...
#>  $ s13: int  1 7 2 4 3 2 2 2 4 3 ...
#>  $ s14: num  3 2 2 2 3 4 2 5 5 2 ...
#>  $ s15: num  1 2 2 2 5 4 2 6 6 2 ...
#>  $ s16: int  2 3 2 2 3 5 4 2 5 2 ...
#>  $ s17: num  1 5 1 4 2 5 6 4 6 2 ...
#>  $ s18: num  1 2 4 4 6 6 4 7 4 3 ...
#>  $ s19: num  2 7 4 3 2 2 4 6 5 4 ...
#>  $ s20: num  1 2 5 2 5 4 5 6 4 3 ...

Build the Measurement Models

methods.model <- '
mlq =~ m1 + m2 + m3 + m4 + m5 + m6 + m8 + m9 + m10
pil =~ p3 + p4 + p8 + p12 + p17 + p20
'

traits.model <- '
meaning =~ m1 + m2 + m5 + m10 + p4 + p12 + p17
purpose =~ m3 + m4 + m6 + m8 + m9 + p3 + p8 + p20
'

Analyze the Measurement Models

methods.fit <- cfa(model = methods.model, 
                   data = meaning.data,
                   std.lv = TRUE)
traits.fit <- cfa(model = traits.model,
                  data = meaning.data,
                  std.lv = TRUE)
#> Warning: lavaan->lav_object_post_check():  
#>    covariance matrix of latent variables is not positive definite ; use 
#>    lavInspect(fit, "cov.lv") to investigate.

lavInspect(traits.fit, "cor.lv")
#>         meanng purpos
#> meaning  1.000       
#> purpose -1.011  1.000

Summarize the Measurement Models

summary(methods.fit, 
        rsquare = TRUE, 
        standardized = TRUE,
        fit.measures = TRUE)
#> lavaan 0.6-19 ended normally after 23 iterations
#> 
#>   Estimator                                         ML
#>   Optimization method                           NLMINB
#>   Number of model parameters                        31
#> 
#>   Number of observations                           567
#> 
#> Model Test User Model:
#>                                                       
#>   Test statistic                              1126.227
#>   Degrees of freedom                                89
#>   P-value (Chi-square)                           0.000
#> 
#> Model Test Baseline Model:
#> 
#>   Test statistic                              4415.161
#>   Degrees of freedom                               105
#>   P-value                                        0.000
#> 
#> User Model versus Baseline Model:
#> 
#>   Comparative Fit Index (CFI)                    0.759
#>   Tucker-Lewis Index (TLI)                       0.716
#> 
#> Loglikelihood and Information Criteria:
#> 
#>   Loglikelihood user model (H0)             -13021.841
#>   Loglikelihood unrestricted model (H1)     -12458.727
#>                                                       
#>   Akaike (AIC)                               26105.681
#>   Bayesian (BIC)                             26240.232
#>   Sample-size adjusted Bayesian (SABIC)      26141.822
#> 
#> Root Mean Square Error of Approximation:
#> 
#>   RMSEA                                          0.143
#>   90 Percent confidence interval - lower         0.136
#>   90 Percent confidence interval - upper         0.151
#>   P-value H_0: RMSEA <= 0.050                    0.000
#>   P-value H_0: RMSEA >= 0.080                    1.000
#> 
#> Standardized Root Mean Square Residual:
#> 
#>   SRMR                                           0.121
#> 
#> Parameter Estimates:
#> 
#>   Standard errors                             Standard
#>   Information                                 Expected
#>   Information saturated (h1) model          Structured
#> 
#> Latent Variables:
#>                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
#>   mlq =~                                                                
#>     m1                1.084    0.048   22.360    0.000    1.084    0.802
#>     m2               -0.578    0.076   -7.656    0.000   -0.578   -0.328
#>     m3               -0.352    0.075   -4.681    0.000   -0.352   -0.204
#>     m4                1.121    0.049   23.095    0.000    1.121    0.819
#>     m5                0.977    0.043   22.480    0.000    0.977    0.805
#>     m6                1.149    0.052   22.247    0.000    1.149    0.799
#>     m8               -0.454    0.073   -6.212    0.000   -0.454   -0.269
#>     m9                0.980    0.057   17.238    0.000    0.980    0.665
#>     m10              -0.906    0.078  -11.552    0.000   -0.906   -0.477
#>   pil =~                                                                
#>     p3                0.776    0.041   19.140    0.000    0.776    0.725
#>     p4                0.799    0.040   20.033    0.000    0.799    0.749
#>     p8                0.626    0.040   15.793    0.000    0.626    0.626
#>     p12               0.890    0.060   14.819    0.000    0.890    0.595
#>     p17               0.663    0.046   14.371    0.000    0.663    0.580
#>     p20               0.923    0.038   24.430    0.000    0.923    0.858
#> 
#> Covariances:
#>                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
#>   mlq ~~                                                                
#>     pil               0.768    0.023   33.098    0.000    0.768    0.768
#> 
#> Variances:
#>                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
#>    .m1                0.653    0.048   13.696    0.000    0.653    0.357
#>    .m2                2.779    0.167   16.631    0.000    2.779    0.893
#>    .m3                2.851    0.170   16.763    0.000    2.851    0.958
#>    .m4                0.616    0.046   13.273    0.000    0.616    0.329
#>    .m5                0.519    0.038   13.631    0.000    0.519    0.352
#>    .m6                0.747    0.054   13.756    0.000    0.747    0.361
#>    .m8                2.656    0.159   16.704    0.000    2.656    0.928
#>    .m9                1.212    0.078   15.468    0.000    1.212    0.558
#>    .m10               2.779    0.170   16.331    0.000    2.779    0.772
#>    .p3                0.543    0.038   14.444    0.000    0.543    0.474
#>    .p4                0.498    0.035   14.060    0.000    0.498    0.438
#>    .p8                0.608    0.039   15.460    0.000    0.608    0.608
#>    .p12               1.444    0.092   15.670    0.000    1.444    0.646
#>    .p17               0.867    0.055   15.758    0.000    0.867    0.663
#>    .p20               0.306    0.028   10.814    0.000    0.306    0.264
#>     mlq               1.000                               1.000    1.000
#>     pil               1.000                               1.000    1.000
#> 
#> R-Square:
#>                    Estimate
#>     m1                0.643
#>     m2                0.107
#>     m3                0.042
#>     m4                0.671
#>     m5                0.648
#>     m6                0.639
#>     m8                0.072
#>     m9                0.442
#>     m10               0.228
#>     p3                0.526
#>     p4                0.562
#>     p8                0.392
#>     p12               0.354
#>     p17               0.337
#>     p20               0.736

summary(traits.fit, 
        rsquare = TRUE, 
        standardized = TRUE,
        fit.measures = TRUE)
#> lavaan 0.6-19 ended normally after 26 iterations
#> 
#>   Estimator                                         ML
#>   Optimization method                           NLMINB
#>   Number of model parameters                        31
#> 
#>   Number of observations                           567
#> 
#> Model Test User Model:
#>                                                       
#>   Test statistic                              1427.750
#>   Degrees of freedom                                89
#>   P-value (Chi-square)                           0.000
#> 
#> Model Test Baseline Model:
#> 
#>   Test statistic                              4415.161
#>   Degrees of freedom                               105
#>   P-value                                        0.000
#> 
#> User Model versus Baseline Model:
#> 
#>   Comparative Fit Index (CFI)                    0.689
#>   Tucker-Lewis Index (TLI)                       0.634
#> 
#> Loglikelihood and Information Criteria:
#> 
#>   Loglikelihood user model (H0)             -13172.602
#>   Loglikelihood unrestricted model (H1)     -12458.727
#>                                                       
#>   Akaike (AIC)                               26407.205
#>   Bayesian (BIC)                             26541.756
#>   Sample-size adjusted Bayesian (SABIC)      26443.345
#> 
#> Root Mean Square Error of Approximation:
#> 
#>   RMSEA                                          0.163
#>   90 Percent confidence interval - lower         0.155
#>   90 Percent confidence interval - upper         0.170
#>   P-value H_0: RMSEA <= 0.050                    0.000
#>   P-value H_0: RMSEA >= 0.080                    1.000
#> 
#> Standardized Root Mean Square Residual:
#> 
#>   SRMR                                           0.127
#> 
#> Parameter Estimates:
#> 
#>   Standard errors                             Standard
#>   Information                                 Expected
#>   Information saturated (h1) model          Structured
#> 
#> Latent Variables:
#>                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
#>   meaning =~                                                            
#>     m1                1.041    0.049   21.190    0.000    1.041    0.770
#>     m2               -0.572    0.075   -7.637    0.000   -0.572   -0.324
#>     m5                0.949    0.044   21.661    0.000    0.949    0.782
#>     m10              -0.872    0.078  -11.166    0.000   -0.872   -0.460
#>     p4                0.741    0.040   18.398    0.000    0.741    0.695
#>     p12               0.887    0.059   15.036    0.000    0.887    0.593
#>     p17               0.644    0.046   14.125    0.000    0.644    0.563
#>   purpose =~                                                            
#>     m3                0.354    0.075    4.756    0.000    0.354    0.205
#>     m4               -1.076    0.049  -21.856    0.000   -1.076   -0.786
#>     m6               -1.106    0.052  -21.158    0.000   -1.106   -0.769
#>     m8                0.437    0.073    6.017    0.000    0.437    0.258
#>     m9               -0.950    0.057  -16.676    0.000   -0.950   -0.644
#>     p3               -0.623    0.042  -14.694    0.000   -0.623   -0.582
#>     p8               -0.536    0.040  -13.301    0.000   -0.536   -0.535
#>     p20              -0.800    0.040  -20.170    0.000   -0.800   -0.743
#> 
#> Covariances:
#>                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
#>   meaning ~~                                                            
#>     purpose          -1.011    0.011  -95.053    0.000   -1.011   -1.011
#> 
#> Variances:
#>                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
#>    .m1                0.744    0.051   14.635    0.000    0.744    0.407
#>    .m2                2.786    0.167   16.678    0.000    2.786    0.895
#>    .m5                0.573    0.040   14.436    0.000    0.573    0.389
#>    .m10               2.839    0.172   16.468    0.000    2.839    0.789
#>    .p4                0.588    0.038   15.483    0.000    0.588    0.517
#>    .p12               1.449    0.090   16.074    0.000    1.449    0.648
#>    .p17               0.893    0.055   16.188    0.000    0.893    0.683
#>    .m3                2.850    0.170   16.777    0.000    2.850    0.958
#>    .m4                0.716    0.050   14.430    0.000    0.716    0.382
#>    .m6                0.846    0.058   14.708    0.000    0.846    0.409
#>    .m8                2.672    0.160   16.739    0.000    2.672    0.933
#>    .m9                1.270    0.080   15.828    0.000    1.270    0.585
#>    .p3                0.758    0.047   16.116    0.000    0.758    0.661
#>    .p8                0.714    0.044   16.274    0.000    0.714    0.713
#>    .p20               0.518    0.034   15.038    0.000    0.518    0.448
#>     meaning           1.000                               1.000    1.000
#>     purpose           1.000                               1.000    1.000
#> 
#> R-Square:
#>                    Estimate
#>     m1                0.593
#>     m2                0.105
#>     m5                0.611
#>     m10               0.211
#>     p4                0.483
#>     p12               0.352
#>     p17               0.317
#>     m3                0.042
#>     m4                0.618
#>     m6                0.591
#>     m8                0.067
#>     m9                0.415
#>     p3                0.339
#>     p8                0.287
#>     p20               0.552

Diagram the Measurement Models

semPaths(methods.fit, 
         whatLabels = "std", 
         layout = "tree", 
         edge.label.cex = 1)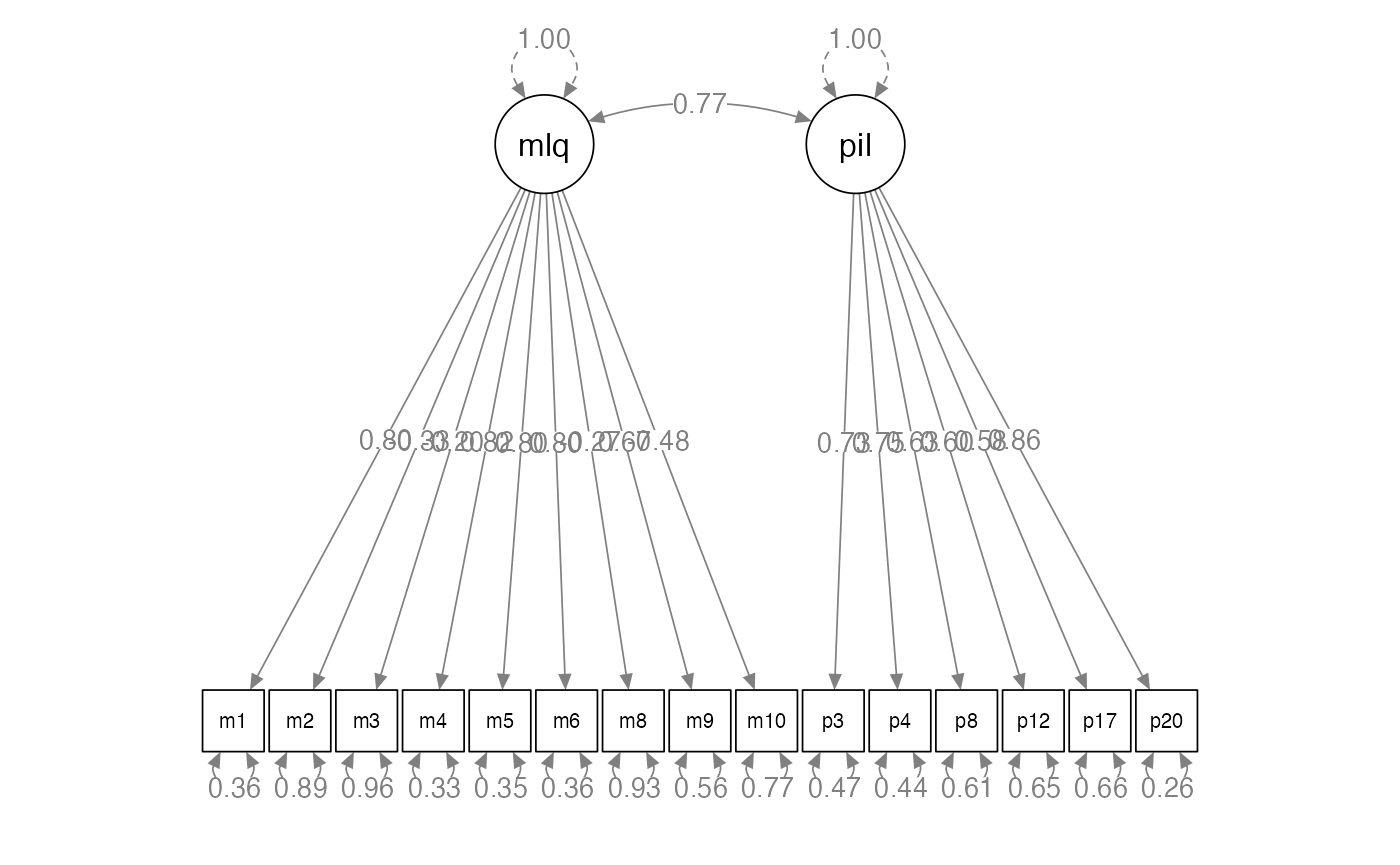


semPaths(traits.fit, 
         whatLabels = "std", 
         layout = "tree", 
         edge.label.cex = 1)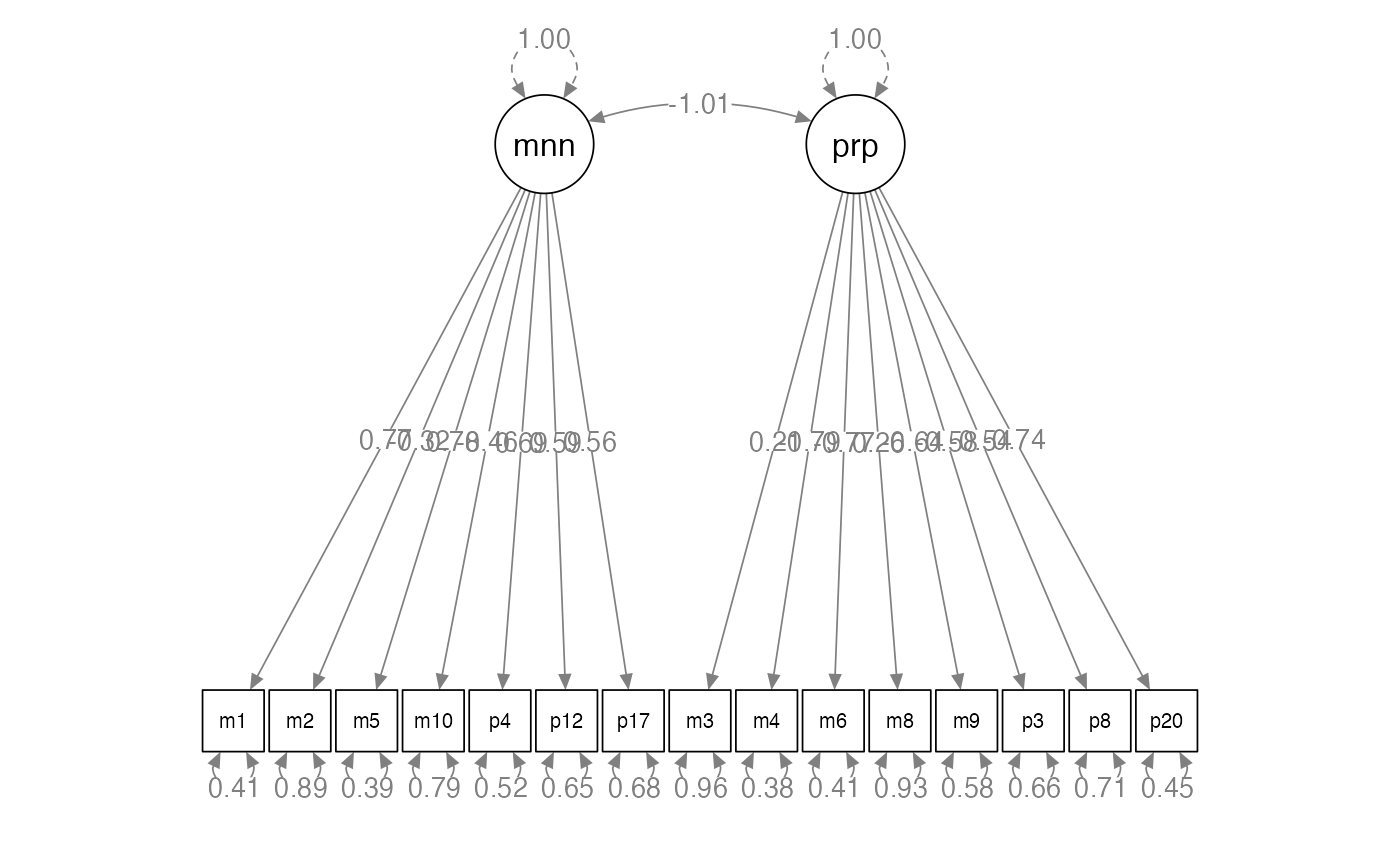

Model 1: Correlated Traits / Correlated Methods

step1.model <- '
mlq =~ m1 + m2 + m3 + m4 + m5 + m6 + m8 + m9 + m10
pil =~ p3 + p4 + p8 + p12 + p17 + p20
meaning =~ m1 + m2 + m5 + m10 + p4 + p12 + p17
purpose =~ m3 + m4 + m6 + m8 + m9 + p3 + p8 + p20

##fix the covariances
mlq ~~ 0*meaning
pil ~~ 0*meaning
mlq ~~ 0*purpose
pil ~~ 0*purpose
'

Model 1: Correlated Traits / Correlated Methods

step1.fit <- cfa(model = step1.model, 
                 data = meaning.data,
                 std.lv = TRUE)

summary(step1.fit, 
        rsquare = TRUE, 
        standardized = TRUE,
        fit.measures = TRUE)
#> lavaan 0.6-19 ended normally after 61 iterations
#> 
#>   Estimator                                         ML
#>   Optimization method                           NLMINB
#>   Number of model parameters                        47
#> 
#>   Number of observations                           567
#> 
#> Model Test User Model:
#>                                                       
#>   Test statistic                               144.899
#>   Degrees of freedom                                73
#>   P-value (Chi-square)                           0.000
#> 
#> Model Test Baseline Model:
#> 
#>   Test statistic                              4415.161
#>   Degrees of freedom                               105
#>   P-value                                        0.000
#> 
#> User Model versus Baseline Model:
#> 
#>   Comparative Fit Index (CFI)                    0.983
#>   Tucker-Lewis Index (TLI)                       0.976
#> 
#> Loglikelihood and Information Criteria:
#> 
#>   Loglikelihood user model (H0)             -12531.177
#>   Loglikelihood unrestricted model (H1)     -12458.727
#>                                                       
#>   Akaike (AIC)                               25156.354
#>   Bayesian (BIC)                             25360.351
#>   Sample-size adjusted Bayesian (SABIC)      25211.148
#> 
#> Root Mean Square Error of Approximation:
#> 
#>   RMSEA                                          0.042
#>   90 Percent confidence interval - lower         0.032
#>   90 Percent confidence interval - upper         0.052
#>   P-value H_0: RMSEA <= 0.050                    0.915
#>   P-value H_0: RMSEA >= 0.080                    0.000
#> 
#> Standardized Root Mean Square Residual:
#> 
#>   SRMR                                           0.024
#> 
#> Parameter Estimates:
#> 
#>   Standard errors                             Standard
#>   Information                                 Expected
#>   Information saturated (h1) model          Structured
#> 
#> Latent Variables:
#>                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
#>   mlq =~                                                                
#>     m1                0.072    0.079    0.912    0.362    0.072    0.053
#>     m2               -1.276    0.071  -17.912    0.000   -1.276   -0.723
#>     m3               -1.364    0.066  -20.783    0.000   -1.364   -0.791
#>     m4               -0.011    0.082   -0.133    0.894   -0.011   -0.008
#>     m5                0.044    0.071    0.624    0.533    0.044    0.036
#>     m6                0.097    0.084    1.146    0.252    0.097    0.067
#>     m8               -1.332    0.065  -20.402    0.000   -1.332   -0.787
#>     m9                0.066    0.081    0.813    0.416    0.066    0.045
#>     m10              -1.302    0.082  -15.838    0.000   -1.302   -0.686
#>   pil =~                                                                
#>     p3                0.708    0.043   16.321    0.000    0.708    0.660
#>     p4                0.441    0.041   10.812    0.000    0.441    0.413
#>     p8                0.463    0.042   10.942    0.000    0.463    0.463
#>     p12               0.344    0.063    5.456    0.000    0.344    0.230
#>     p17               0.255    0.049    5.236    0.000    0.255    0.223
#>     p20               0.628    0.038   16.314    0.000    0.628    0.583
#>   meaning =~                                                            
#>     m1               -1.090    0.049  -22.359    0.000   -1.090   -0.806
#>     m2                0.414    0.111    3.728    0.000    0.414    0.234
#>     m5               -0.987    0.044  -22.682    0.000   -0.987   -0.813
#>     m10               0.745    0.115    6.503    0.000    0.745    0.392
#>     p4               -0.658    0.042  -15.527    0.000   -0.658   -0.617
#>     p12              -0.824    0.061  -13.569    0.000   -0.824   -0.551
#>     p17              -0.609    0.047  -13.032    0.000   -0.609   -0.532
#>   purpose =~                                                            
#>     m3               -0.157    0.115   -1.369    0.171   -0.157   -0.091
#>     m4                1.149    0.048   23.832    0.000    1.149    0.839
#>     m6                1.147    0.052   21.965    0.000    1.147    0.798
#>     m8               -0.273    0.112   -2.435    0.015   -0.273   -0.161
#>     m9                0.980    0.057   17.147    0.000    0.980    0.665
#>     p3                0.486    0.045   10.692    0.000    0.486    0.453
#>     p8                0.441    0.042   10.443    0.000    0.441    0.441
#>     p20               0.693    0.043   16.270    0.000    0.693    0.643
#> 
#> Covariances:
#>                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
#>   mlq ~~                                                                
#>     meaning           0.000                               0.000    0.000
#>   pil ~~                                                                
#>     meaning           0.000                               0.000    0.000
#>   mlq ~~                                                                
#>     purpose           0.000                               0.000    0.000
#>   pil ~~                                                                
#>     purpose           0.000                               0.000    0.000
#>   mlq ~~                                                                
#>     pil               0.147    0.083    1.763    0.078    0.147    0.147
#>   meaning ~~                                                            
#>     purpose          -0.987    0.011  -92.538    0.000   -0.987   -0.987
#> 
#> Variances:
#>                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
#>    .m1                0.635    0.048   13.361    0.000    0.635    0.347
#>    .m2                1.316    0.100   13.204    0.000    1.316    0.423
#>    .m3                1.089    0.094   11.580    0.000    1.089    0.366
#>    .m4                0.553    0.045   12.200    0.000    0.553    0.295
#>    .m5                0.498    0.038   13.148    0.000    0.498    0.338
#>    .m6                0.743    0.055   13.632    0.000    0.743    0.359
#>    .m8                1.015    0.088   11.561    0.000    1.015    0.355
#>    .m9                1.208    0.078   15.433    0.000    1.208    0.556
#>    .m10               1.352    0.104   13.050    0.000    1.352    0.375
#>    .p3                0.411    0.041    9.997    0.000    0.411    0.358
#>    .p4                0.511    0.035   14.556    0.000    0.511    0.449
#>    .p8                0.592    0.039   15.029    0.000    0.592    0.591
#>    .p12               1.440    0.090   16.075    0.000    1.440    0.644
#>    .p17               0.872    0.054   16.150    0.000    0.872    0.667
#>    .p20               0.287    0.030    9.490    0.000    0.287    0.247
#>     mlq               1.000                               1.000    1.000
#>     pil               1.000                               1.000    1.000
#>     meaning           1.000                               1.000    1.000
#>     purpose           1.000                               1.000    1.000
#> 
#> R-Square:
#>                    Estimate
#>     m1                0.653
#>     m2                0.577
#>     m3                0.634
#>     m4                0.705
#>     m5                0.662
#>     m6                0.641
#>     m8                0.645
#>     m9                0.444
#>     m10               0.625
#>     p3                0.642
#>     p4                0.551
#>     p8                0.409
#>     p12               0.356
#>     p17               0.333
#>     p20               0.753

Model 1: Correlated Traits / Correlated Methods

semPaths(step1.fit, 
         whatLabels = "std", 
         layout = "tree", 
         edge.label.cex = 1)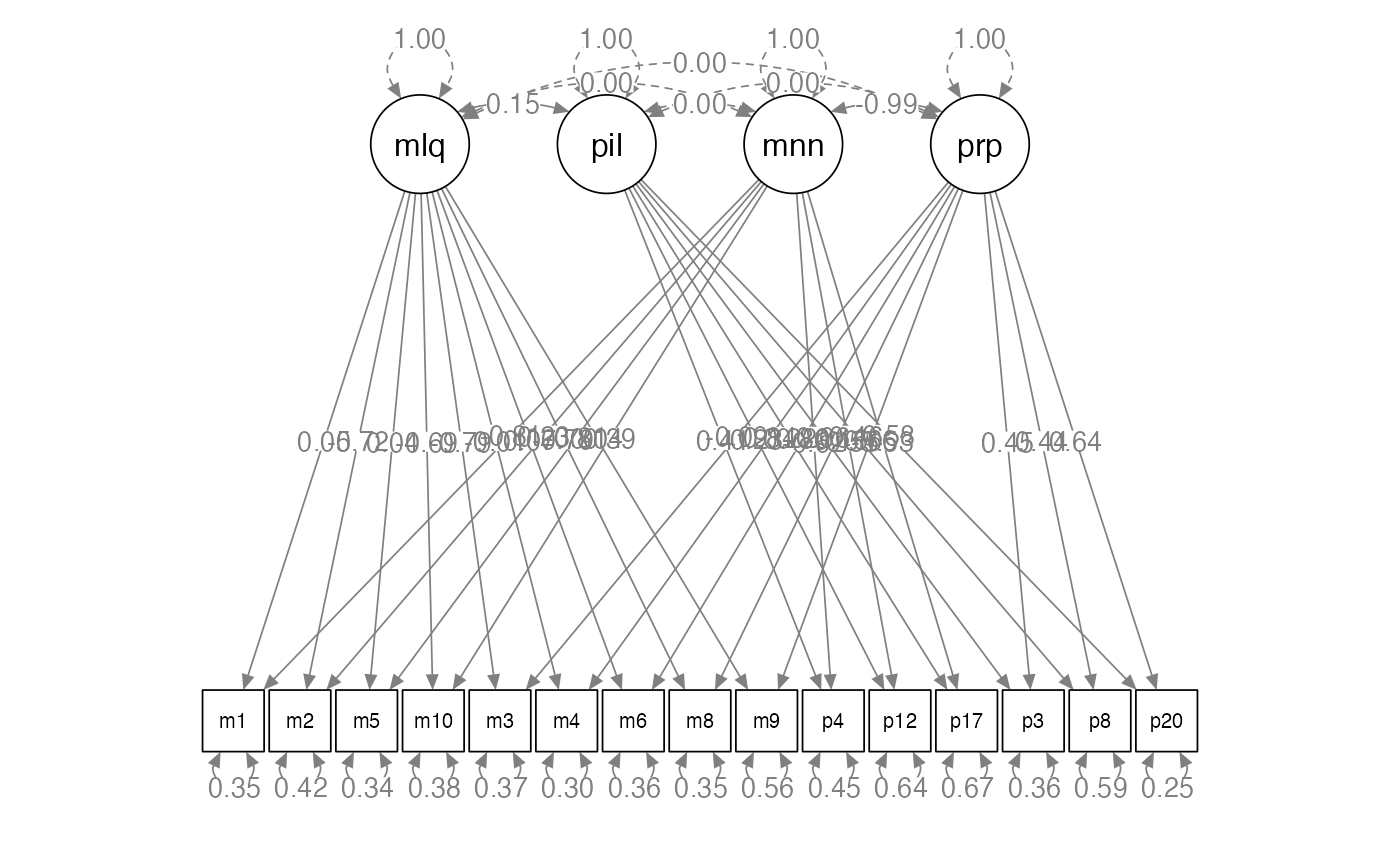

Model 2: No Traits / Correlated Methods

Completely delete the trait latent side.
We are testing the methods only model.
Model 1 versus Model 2
- Convergent validity: Independent measures of the same trait are correlated
- You want Model 2 to be worse than Model 1.
- Model 1 has both traits and methods, while Model 2 only has methods. If Model 2 is good, that means that methods is the best estimate for the data and that traits are not useful (that’s bad).

Model 2: No Traits / Correlated Methods

Model 2 is worse than Model 1, implying we need the traits to interpret the data, supporting convergent validity.

##model 2 is the methods model 
##we've already checked it out
anova(step1.fit, methods.fit)
#> 
#> Chi-Squared Difference Test
#> 
#>             Df   AIC   BIC  Chisq Chisq diff  RMSEA Df diff Pr(>Chisq)    
#> step1.fit   73 25156 25360  144.9                                         
#> methods.fit 89 26106 26240 1126.2     981.33 0.3262      16  < 2.2e-16 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

fitmeasures(step1.fit, "cfi") 
#>   cfi 
#> 0.983
fitmeasures(methods.fit, "cfi")
#>   cfi 
#> 0.759

Model 3: Perfectly Correlated Traits / Freely Correlated Methods

In this model, we will include both traits and methods.
We will set the covariances for traits to one.
By setting these to one, we are testing if the traits are exactly the same, which would indicate we are not measuring separate variables.
Discriminant validity: you want traits to measure different things.
Therefore, we want Model 1 to be better than Model 3.

Model 3: Perfectly Correlated Traits / Freely Correlated Methods

step3.model <- '
mlq =~ m1 + m2 + m3 + m4 + m5 + m6 + m8 + m9 + m10
pil =~ p3 + p4 + p8 + p12 + p17 + p20
meaning =~ m1 + m2 + m5 + m10 + p4 + p12 + p17
purpose =~ m3 + m4 + m6 + m8 + m9 + p3 + p8 + p20

##fix the covariances
mlq ~~ 0*meaning
pil ~~ 0*meaning
mlq ~~ 0*purpose
pil ~~ 0*purpose
meaning ~~ 1*purpose
'

Model 3: Perfectly Correlated Traits / Freely Correlated Methods

step3.fit <- cfa(model = step3.model,
                 data = meaning.data,
                 std.lv = TRUE)

summary(step3.fit, 
        rsquare = TRUE, 
        standardized = TRUE, 
        fit.measure = TRUE)
#> lavaan 0.6-19 ended normally after 47 iterations
#> 
#>   Estimator                                         ML
#>   Optimization method                           NLMINB
#>   Number of model parameters                        46
#> 
#>   Number of observations                           567
#> 
#> Model Test User Model:
#>                                                       
#>   Test statistic                               146.376
#>   Degrees of freedom                                74
#>   P-value (Chi-square)                           0.000
#> 
#> Model Test Baseline Model:
#> 
#>   Test statistic                              4415.161
#>   Degrees of freedom                               105
#>   P-value                                        0.000
#> 
#> User Model versus Baseline Model:
#> 
#>   Comparative Fit Index (CFI)                    0.983
#>   Tucker-Lewis Index (TLI)                       0.976
#> 
#> Loglikelihood and Information Criteria:
#> 
#>   Loglikelihood user model (H0)             -12531.915
#>   Loglikelihood unrestricted model (H1)     -12458.727
#>                                                       
#>   Akaike (AIC)                               25155.830
#>   Bayesian (BIC)                             25355.487
#>   Sample-size adjusted Bayesian (SABIC)      25209.458
#> 
#> Root Mean Square Error of Approximation:
#> 
#>   RMSEA                                          0.042
#>   90 Percent confidence interval - lower         0.032
#>   90 Percent confidence interval - upper         0.051
#>   P-value H_0: RMSEA <= 0.050                    0.920
#>   P-value H_0: RMSEA >= 0.080                    0.000
#> 
#> Standardized Root Mean Square Residual:
#> 
#>   SRMR                                           0.024
#> 
#> Parameter Estimates:
#> 
#>   Standard errors                             Standard
#>   Information                                 Expected
#>   Information saturated (h1) model          Structured
#> 
#> Latent Variables:
#>                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
#>   mlq =~                                                                
#>     m1                0.072    0.078    0.922    0.357    0.072    0.053
#>     m2               -1.276    0.071  -17.952    0.000   -1.276   -0.723
#>     m3               -1.364    0.066  -20.794    0.000   -1.364   -0.791
#>     m4               -0.011    0.080   -0.134    0.894   -0.011   -0.008
#>     m5                0.045    0.070    0.635    0.525    0.045    0.037
#>     m6                0.096    0.083    1.164    0.245    0.096    0.067
#>     m8               -1.331    0.065  -20.426    0.000   -1.331   -0.787
#>     m9                0.065    0.080    0.818    0.413    0.065    0.044
#>     m10              -1.302    0.082  -15.883    0.000   -1.302   -0.686
#>   pil =~                                                                
#>     p3                0.710    0.043   16.354    0.000    0.710    0.663
#>     p4                0.436    0.041   10.710    0.000    0.436    0.409
#>     p8                0.464    0.042   10.963    0.000    0.464    0.464
#>     p12               0.339    0.063    5.380    0.000    0.339    0.227
#>     p17               0.251    0.049    5.152    0.000    0.251    0.220
#>     p20               0.627    0.039   16.280    0.000    0.627    0.583
#>   meaning =~                                                            
#>     m1                1.087    0.049   22.366    0.000    1.087    0.804
#>     m2               -0.409    0.110   -3.716    0.000   -0.409   -0.232
#>     m5                0.984    0.043   22.665    0.000    0.984    0.810
#>     m10              -0.743    0.114   -6.543    0.000   -0.743   -0.391
#>     p4                0.654    0.042   15.439    0.000    0.654    0.613
#>     p12               0.819    0.061   13.511    0.000    0.819    0.548
#>     p17               0.606    0.047   12.981    0.000    0.606    0.530
#>   purpose =~                                                            
#>     m3               -0.155    0.113   -1.364    0.173   -0.155   -0.090
#>     m4                1.145    0.048   23.825    0.000    1.145    0.836
#>     m6                1.142    0.052   21.918    0.000    1.142    0.794
#>     m8               -0.270    0.111   -2.440    0.015   -0.270   -0.160
#>     m9                0.978    0.057   17.147    0.000    0.978    0.664
#>     p3                0.482    0.045   10.631    0.000    0.482    0.450
#>     p8                0.440    0.042   10.424    0.000    0.440    0.440
#>     p20               0.689    0.043   16.198    0.000    0.689    0.640
#> 
#> Covariances:
#>                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
#>   mlq ~~                                                                
#>     meaning           0.000                               0.000    0.000
#>   pil ~~                                                                
#>     meaning           0.000                               0.000    0.000
#>   mlq ~~                                                                
#>     purpose           0.000                               0.000    0.000
#>   pil ~~                                                                
#>     purpose           0.000                               0.000    0.000
#>   meaning ~~                                                            
#>     purpose           1.000                               1.000    1.000
#>   mlq ~~                                                                
#>     pil               0.146    0.082    1.785    0.074    0.146    0.146
#> 
#> Variances:
#>                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
#>    .m1                0.641    0.047   13.742    0.000    0.641    0.351
#>    .m2                1.319    0.100   13.211    0.000    1.319    0.424
#>    .m3                1.090    0.094   11.582    0.000    1.090    0.366
#>    .m4                0.563    0.044   12.730    0.000    0.563    0.301
#>    .m5                0.505    0.037   13.580    0.000    0.505    0.342
#>    .m6                0.754    0.054   13.959    0.000    0.754    0.365
#>    .m8                1.017    0.088   11.584    0.000    1.017    0.355
#>    .m9                1.212    0.078   15.528    0.000    1.212    0.558
#>    .m10               1.353    0.103   13.078    0.000    1.353    0.376
#>    .p3                0.409    0.041    9.882    0.000    0.409    0.357
#>    .p4                0.520    0.035   14.875    0.000    0.520    0.457
#>    .p8                0.592    0.039   15.020    0.000    0.592    0.592
#>    .p12               1.449    0.090   16.172    0.000    1.449    0.648
#>    .p17               0.877    0.054   16.236    0.000    0.877    0.671
#>    .p20               0.290    0.030    9.587    0.000    0.290    0.251
#>     mlq               1.000                               1.000    1.000
#>     pil               1.000                               1.000    1.000
#>     meaning           1.000                               1.000    1.000
#>     purpose           1.000                               1.000    1.000
#> 
#> R-Square:
#>                    Estimate
#>     m1                0.649
#>     m2                0.576
#>     m3                0.634
#>     m4                0.699
#>     m5                0.658
#>     m6                0.635
#>     m8                0.645
#>     m9                0.442
#>     m10               0.624
#>     p3                0.643
#>     p4                0.543
#>     p8                0.408
#>     p12               0.352
#>     p17               0.329
#>     p20               0.749

Model 3: Perfectly Correlated Traits / Freely Correlated Methods

semPaths(step3.fit, 
         whatLabels = "std", 
         layout = "tree", 
         edge.label.cex = 1)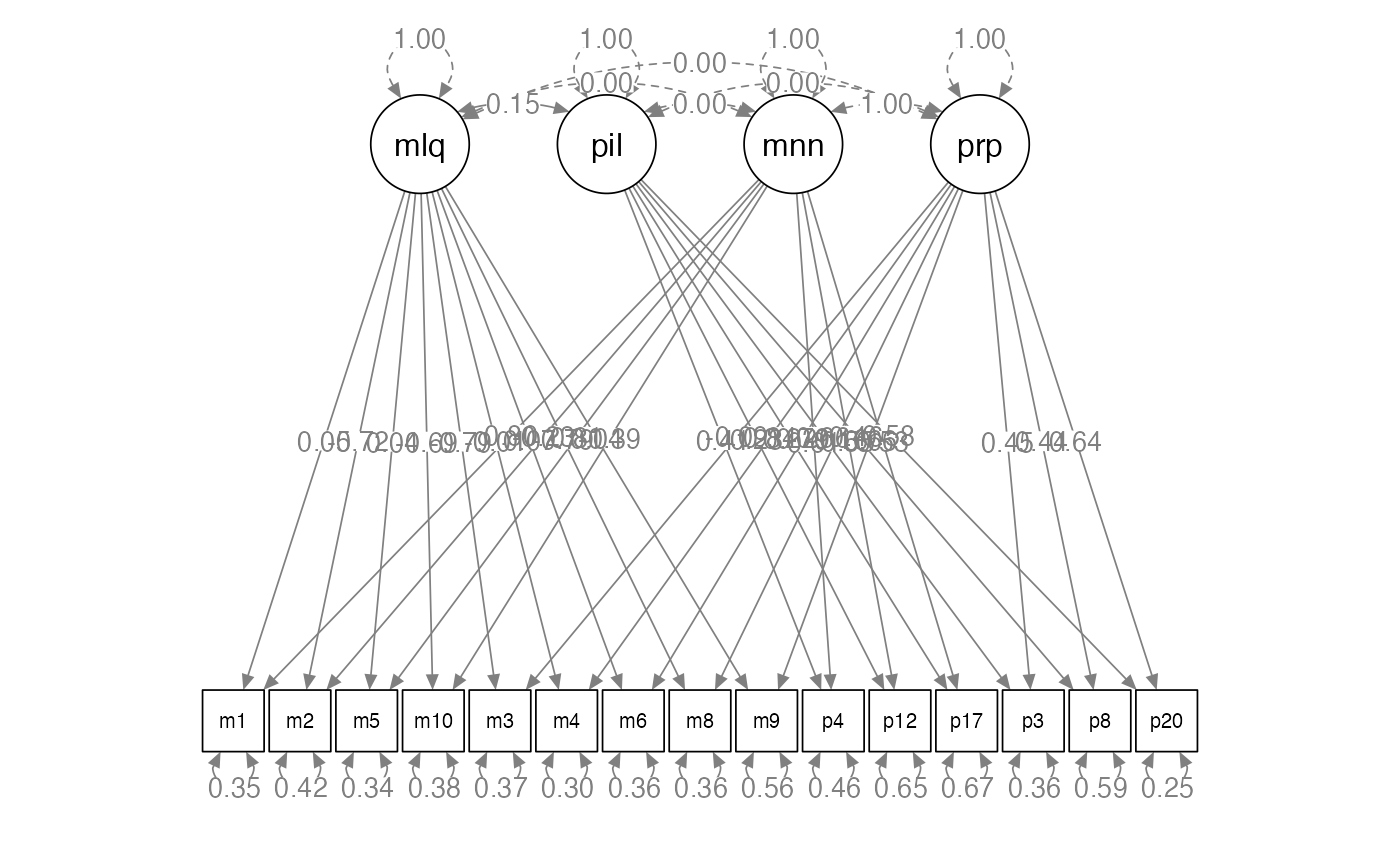

Model 3: Perfectly Correlated Traits / Freely Correlated Methods

Oh no! These models are exactly the same.
This result implies that our traits are not discriminating (meaning = purpose).

anova(step1.fit, step3.fit)
#> 
#> Chi-Squared Difference Test
#> 
#>           Df   AIC   BIC  Chisq Chisq diff    RMSEA Df diff Pr(>Chisq)
#> step1.fit 73 25156 25360 144.90                                       
#> step3.fit 74 25156 25356 146.38     1.4763 0.028983       1     0.2244

fitmeasures(step1.fit, "cfi")
#>   cfi 
#> 0.983
fitmeasures(step3.fit, "cfi")
#>   cfi 
#> 0.983

Model 4: Freely Correlated Traits / Uncorrelated Methods

In this last step, we set the covariances between methods to zero.
This result would imply that the methods are not measuring exactly the same way.
Discriminant validity of the methods: different measures each assess different parts of the latent variables
You want to find that Model 1 and Model 4 are equal.

Model 4: Freely Correlated Traits / Uncorrelated Methods

step4.model <- '
mlq =~ m1 + m2 + m3 + m4 + m5 + m6 + m8 + m9 + m10
pil =~ p3 + p4 + p8 + p12 + p17 + p20
meaning =~ m1 + m2 + m5 + m10 + p4 + p12 + p17
purpose =~ m3 + m4 + m6 + m8 + m9 + p3 + p8 + p20

##fix the covariances
mlq ~~ 0*meaning
pil ~~ 0*meaning
mlq ~~ 0*purpose
pil ~~ 0*purpose
pil ~~ 0*mlq
'

Model 4: Freely Correlated Traits / Uncorrelated Methods

step4.fit <- cfa(model = step4.model, 
                  data = meaning.data,
                  std.lv = TRUE)

summary(step4.fit, 
        rsquare = TRUE, 
        standardized = TRUE, 
        fit.measure = TRUE)
#> lavaan 0.6-19 ended normally after 38 iterations
#> 
#>   Estimator                                         ML
#>   Optimization method                           NLMINB
#>   Number of model parameters                        46
#> 
#>   Number of observations                           567
#> 
#> Model Test User Model:
#>                                                       
#>   Test statistic                               147.707
#>   Degrees of freedom                                74
#>   P-value (Chi-square)                           0.000
#> 
#> Model Test Baseline Model:
#> 
#>   Test statistic                              4415.161
#>   Degrees of freedom                               105
#>   P-value                                        0.000
#> 
#> User Model versus Baseline Model:
#> 
#>   Comparative Fit Index (CFI)                    0.983
#>   Tucker-Lewis Index (TLI)                       0.976
#> 
#> Loglikelihood and Information Criteria:
#> 
#>   Loglikelihood user model (H0)             -12532.581
#>   Loglikelihood unrestricted model (H1)     -12458.727
#>                                                       
#>   Akaike (AIC)                               25157.162
#>   Bayesian (BIC)                             25356.818
#>   Sample-size adjusted Bayesian (SABIC)      25210.790
#> 
#> Root Mean Square Error of Approximation:
#> 
#>   RMSEA                                          0.042
#>   90 Percent confidence interval - lower         0.032
#>   90 Percent confidence interval - upper         0.052
#>   P-value H_0: RMSEA <= 0.050                    0.910
#>   P-value H_0: RMSEA >= 0.080                    0.000
#> 
#> Standardized Root Mean Square Residual:
#> 
#>   SRMR                                           0.025
#> 
#> Parameter Estimates:
#> 
#>   Standard errors                             Standard
#>   Information                                 Expected
#>   Information saturated (h1) model          Structured
#> 
#> Latent Variables:
#>                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
#>   mlq =~                                                                
#>     m1                0.028    0.056    0.494    0.621    0.028    0.020
#>     m2                1.235    0.069   18.000    0.000    1.235    0.700
#>     m3                1.346    0.066   20.543    0.000    1.346    0.780
#>     m4                0.117    0.056    2.067    0.039    0.117    0.085
#>     m5                0.045    0.050    0.907    0.365    0.045    0.037
#>     m6                0.010    0.060    0.162    0.871    0.010    0.007
#>     m8                1.301    0.064   20.254    0.000    1.301    0.769
#>     m9                0.025    0.063    0.396    0.692    0.025    0.017
#>     m10               1.226    0.074   16.589    0.000    1.226    0.646
#>   pil =~                                                                
#>     p3                0.703    0.043   16.242    0.000    0.703    0.656
#>     p4                0.435    0.040   10.835    0.000    0.435    0.408
#>     p8                0.461    0.042   10.945    0.000    0.461    0.461
#>     p12               0.332    0.062    5.326    0.000    0.332    0.222
#>     p17               0.261    0.049    5.384    0.000    0.261    0.228
#>     p20               0.617    0.038   16.364    0.000    0.617    0.573
#>   meaning =~                                                            
#>     m1                1.092    0.048   22.555    0.000    1.092    0.808
#>     m2               -0.528    0.088   -6.002    0.000   -0.528   -0.299
#>     m5                0.987    0.043   22.747    0.000    0.987    0.813
#>     m10              -0.861    0.091   -9.510    0.000   -0.861   -0.453
#>     p4                0.662    0.042   15.744    0.000    0.662    0.620
#>     p12               0.828    0.060   13.708    0.000    0.828    0.554
#>     p17               0.602    0.047   12.897    0.000    0.602    0.526
#>   purpose =~                                                            
#>     m3                0.282    0.090    3.134    0.002    0.282    0.163
#>     m4               -1.143    0.048  -23.610    0.000   -1.143   -0.835
#>     m6               -1.151    0.052  -22.272    0.000   -1.151   -0.800
#>     m8                0.394    0.087    4.509    0.000    0.394    0.233
#>     m9               -0.982    0.057  -17.277    0.000   -0.982   -0.666
#>     p3               -0.493    0.045  -11.050    0.000   -0.493   -0.460
#>     p8               -0.445    0.042  -10.624    0.000   -0.445   -0.444
#>     p20              -0.701    0.042  -16.729    0.000   -0.701   -0.650
#> 
#> Covariances:
#>                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
#>   mlq ~~                                                                
#>     meaning           0.000                               0.000    0.000
#>   pil ~~                                                                
#>     meaning           0.000                               0.000    0.000
#>   mlq ~~                                                                
#>     purpose           0.000                               0.000    0.000
#>   pil ~~                                                                
#>     purpose           0.000                               0.000    0.000
#>   mlq ~~                                                                
#>     pil               0.000                               0.000    0.000
#>   meaning ~~                                                            
#>     purpose          -0.988    0.010  -95.659    0.000   -0.988   -0.988
#> 
#> Variances:
#>                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
#>    .m1                0.635    0.047   13.375    0.000    0.635    0.347
#>    .m2                1.311    0.100   13.172    0.000    1.311    0.421
#>    .m3                1.085    0.094   11.539    0.000    1.085    0.365
#>    .m4                0.554    0.045   12.225    0.000    0.554    0.295
#>    .m5                0.498    0.038   13.172    0.000    0.498    0.338
#>    .m6                0.743    0.054   13.632    0.000    0.743    0.359
#>    .m8                1.014    0.088   11.541    0.000    1.014    0.354
#>    .m9                1.207    0.078   15.432    0.000    1.207    0.556
#>    .m10               1.359    0.104   13.072    0.000    1.359    0.377
#>    .p3                0.410    0.041    9.904    0.000    0.410    0.357
#>    .p4                0.512    0.035   14.562    0.000    0.512    0.449
#>    .p8                0.591    0.039   14.988    0.000    0.591    0.590
#>    .p12               1.440    0.089   16.097    0.000    1.440    0.644
#>    .p17               0.878    0.054   16.167    0.000    0.878    0.671
#>    .p20               0.289    0.030    9.567    0.000    0.289    0.249
#>     mlq               1.000                               1.000    1.000
#>     pil               1.000                               1.000    1.000
#>     meaning           1.000                               1.000    1.000
#>     purpose           1.000                               1.000    1.000
#> 
#> R-Square:
#>                    Estimate
#>     m1                0.653
#>     m2                0.579
#>     m3                0.635
#>     m4                0.705
#>     m5                0.662
#>     m6                0.641
#>     m8                0.646
#>     m9                0.444
#>     m10               0.623
#>     p3                0.643
#>     p4                0.551
#>     p8                0.410
#>     p12               0.356
#>     p17               0.329
#>     p20               0.751

Model 4: Freely Correlated Traits / Uncorrelated Methods

semPaths(step4.fit, 
         whatLabels = "std", 
         layout = "tree", 
         edge.label.cex = 1)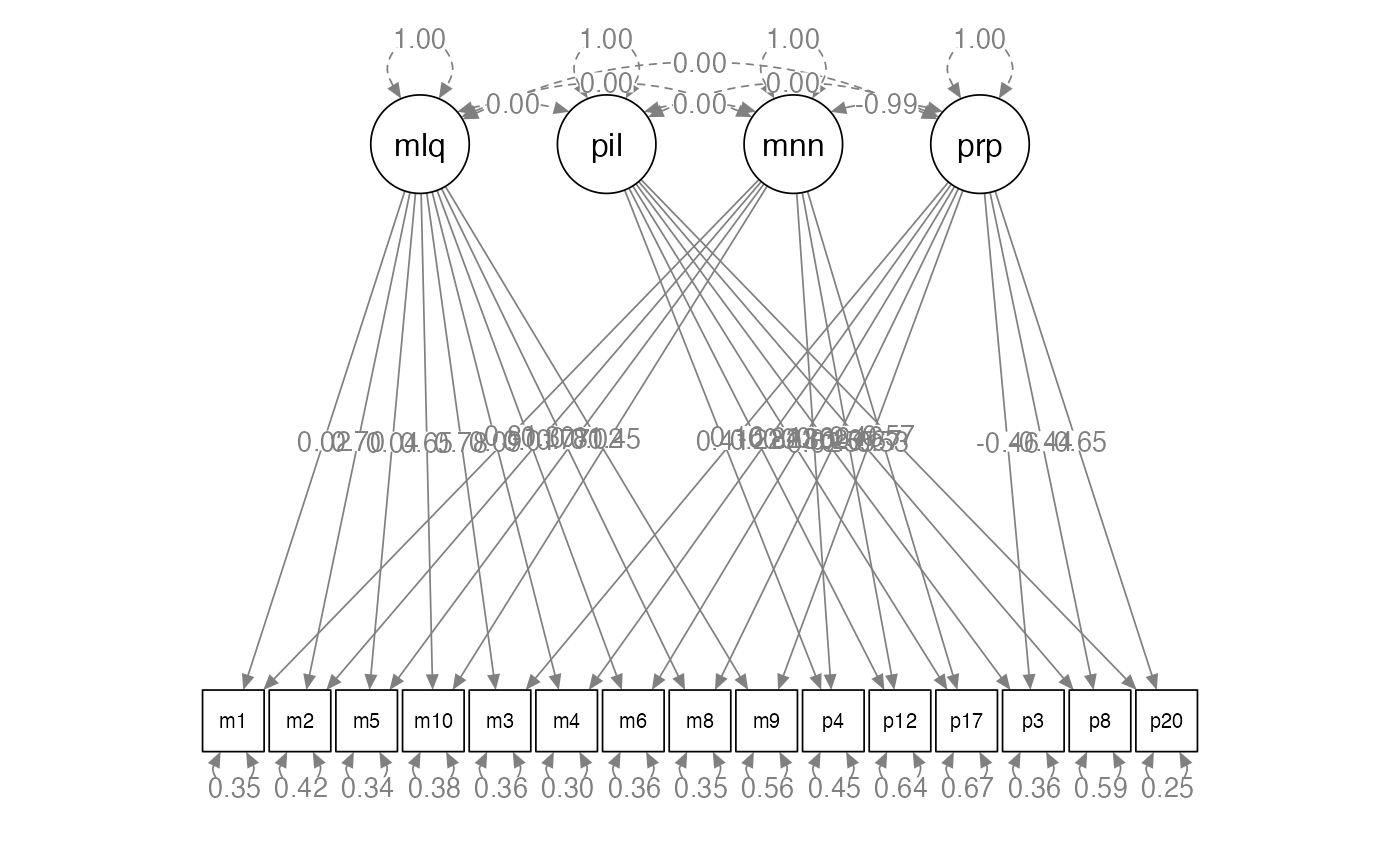

Model 4: Freely Correlated Traits / Uncorrelated Methods

These two models are equal, which is a good thing, indicating our two scales assess these measures differently.

anova(step1.fit, step4.fit)
#> 
#> Chi-Squared Difference Test
#> 
#>           Df   AIC   BIC  Chisq Chisq diff    RMSEA Df diff Pr(>Chisq)  
#> step1.fit 73 25156 25360 144.90                                         
#> step4.fit 74 25157 25357 147.71      2.808 0.056469       1     0.0938 .
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

fitmeasures(step1.fit, "cfi")
#>   cfi 
#> 0.983
fitmeasures(step4.fit, "cfi")
#>   cfi 
#> 0.983

Correlated Uniqueness

Another type of analysis would be to examine for convergent and discriminant validity using correlated uniqueness approach.
You would create the traits side of the model, which is the same as the first traits.model we created.
Instead of using latent variables to predict each observed items for the measurement side, we would simply correlate the error terms for each of the observed items on the same scale.
From this model, you would interpret parameters (which you can also do with Model 1 from the other analysis).

Interpreting Parameters

Convergent validity: the trait loadings are higher than the methods loadings.
This finding would tell you if the trait effect is greater than the method effects.

parameterestimates(step1.fit, standardized = T)
#>        lhs op     rhs    est    se       z pvalue ci.lower ci.upper std.lv
#> 1      mlq =~      m1  0.072 0.079   0.912  0.362   -0.082    0.226  0.072
#> 2      mlq =~      m2 -1.276 0.071 -17.912  0.000   -1.415   -1.136 -1.276
#> 3      mlq =~      m3 -1.364 0.066 -20.783  0.000   -1.493   -1.236 -1.364
#> 4      mlq =~      m4 -0.011 0.082  -0.133  0.894   -0.171    0.150 -0.011
#> 5      mlq =~      m5  0.044 0.071   0.624  0.533   -0.095    0.183  0.044
#> 6      mlq =~      m6  0.097 0.084   1.146  0.252   -0.069    0.262  0.097
#> 7      mlq =~      m8 -1.332 0.065 -20.402  0.000   -1.460   -1.204 -1.332
#> 8      mlq =~      m9  0.066 0.081   0.813  0.416   -0.093    0.225  0.066
#> 9      mlq =~     m10 -1.302 0.082 -15.838  0.000   -1.463   -1.141 -1.302
#> 10     pil =~      p3  0.708 0.043  16.321  0.000    0.623    0.793  0.708
#> 11     pil =~      p4  0.441 0.041  10.812  0.000    0.361    0.521  0.441
#> 12     pil =~      p8  0.463 0.042  10.942  0.000    0.380    0.546  0.463
#> 13     pil =~     p12  0.344 0.063   5.456  0.000    0.220    0.467  0.344
#> 14     pil =~     p17  0.255 0.049   5.236  0.000    0.160    0.351  0.255
#> 15     pil =~     p20  0.628 0.038  16.314  0.000    0.552    0.703  0.628
#> 16 meaning =~      m1 -1.090 0.049 -22.359  0.000   -1.186   -0.995 -1.090
#> 17 meaning =~      m2  0.414 0.111   3.728  0.000    0.196    0.631  0.414
#> 18 meaning =~      m5 -0.987 0.044 -22.682  0.000   -1.072   -0.902 -0.987
#> 19 meaning =~     m10  0.745 0.115   6.503  0.000    0.520    0.969  0.745
#> 20 meaning =~      p4 -0.658 0.042 -15.527  0.000   -0.741   -0.575 -0.658
#> 21 meaning =~     p12 -0.824 0.061 -13.569  0.000   -0.943   -0.705 -0.824
#> 22 meaning =~     p17 -0.609 0.047 -13.032  0.000   -0.701   -0.517 -0.609
#> 23 purpose =~      m3 -0.157 0.115  -1.369  0.171   -0.382    0.068 -0.157
#> 24 purpose =~      m4  1.149 0.048  23.832  0.000    1.055    1.244  1.149
#> 25 purpose =~      m6  1.147 0.052  21.965  0.000    1.045    1.249  1.147
#> 26 purpose =~      m8 -0.273 0.112  -2.435  0.015   -0.492   -0.053 -0.273
#> 27 purpose =~      m9  0.980 0.057  17.147  0.000    0.868    1.092  0.980
#> 28 purpose =~      p3  0.486 0.045  10.692  0.000    0.397    0.575  0.486
#> 29 purpose =~      p8  0.441 0.042  10.443  0.000    0.359    0.524  0.441
#> 30 purpose =~     p20  0.693 0.043  16.270  0.000    0.609    0.776  0.693
#> 31     mlq ~~ meaning  0.000 0.000      NA     NA    0.000    0.000  0.000
#> 32     pil ~~ meaning  0.000 0.000      NA     NA    0.000    0.000  0.000
#> 33     mlq ~~ purpose  0.000 0.000      NA     NA    0.000    0.000  0.000
#> 34     pil ~~ purpose  0.000 0.000      NA     NA    0.000    0.000  0.000
#> 35      m1 ~~      m1  0.635 0.048  13.361  0.000    0.542    0.728  0.635
#> 36      m2 ~~      m2  1.316 0.100  13.204  0.000    1.121    1.512  1.316
#> 37      m3 ~~      m3  1.089 0.094  11.580  0.000    0.905    1.274  1.089
#> 38      m4 ~~      m4  0.553 0.045  12.200  0.000    0.464    0.642  0.553
#> 39      m5 ~~      m5  0.498 0.038  13.148  0.000    0.424    0.572  0.498
#> 40      m6 ~~      m6  0.743 0.055  13.632  0.000    0.636    0.850  0.743
#> 41      m8 ~~      m8  1.015 0.088  11.561  0.000    0.843    1.187  1.015
#> 42      m9 ~~      m9  1.208 0.078  15.433  0.000    1.054    1.361  1.208
#> 43     m10 ~~     m10  1.352 0.104  13.050  0.000    1.149    1.556  1.352
#> 44      p3 ~~      p3  0.411 0.041   9.997  0.000    0.331    0.492  0.411
#> 45      p4 ~~      p4  0.511 0.035  14.556  0.000    0.443    0.580  0.511
#> 46      p8 ~~      p8  0.592 0.039  15.029  0.000    0.515    0.670  0.592
#> 47     p12 ~~     p12  1.440 0.090  16.075  0.000    1.264    1.615  1.440
#> 48     p17 ~~     p17  0.872 0.054  16.150  0.000    0.766    0.978  0.872
#> 49     p20 ~~     p20  0.287 0.030   9.490  0.000    0.228    0.346  0.287
#> 50     mlq ~~     mlq  1.000 0.000      NA     NA    1.000    1.000  1.000
#> 51     pil ~~     pil  1.000 0.000      NA     NA    1.000    1.000  1.000
#> 52 meaning ~~ meaning  1.000 0.000      NA     NA    1.000    1.000  1.000
#> 53 purpose ~~ purpose  1.000 0.000      NA     NA    1.000    1.000  1.000
#> 54     mlq ~~     pil  0.147 0.083   1.763  0.078   -0.016    0.310  0.147
#> 55 meaning ~~ purpose -0.987 0.011 -92.538  0.000   -1.008   -0.967 -0.987
#>    std.all
#> 1    0.053
#> 2   -0.723
#> 3   -0.791
#> 4   -0.008
#> 5    0.036
#> 6    0.067
#> 7   -0.787
#> 8    0.045
#> 9   -0.686
#> 10   0.660
#> 11   0.413
#> 12   0.463
#> 13   0.230
#> 14   0.223
#> 15   0.583
#> 16  -0.806
#> 17   0.234
#> 18  -0.813
#> 19   0.392
#> 20  -0.617
#> 21  -0.551
#> 22  -0.532
#> 23  -0.091
#> 24   0.839
#> 25   0.798
#> 26  -0.161
#> 27   0.665
#> 28   0.453
#> 29   0.441
#> 30   0.643
#> 31   0.000
#> 32   0.000
#> 33   0.000
#> 34   0.000
#> 35   0.347
#> 36   0.423
#> 37   0.366
#> 38   0.295
#> 39   0.338
#> 40   0.359
#> 41   0.355
#> 42   0.556
#> 43   0.375
#> 44   0.358
#> 45   0.449
#> 46   0.591
#> 47   0.644
#> 48   0.667
#> 49   0.247
#> 50   1.000
#> 51   1.000
#> 52   1.000
#> 53   1.000
#> 54   0.147
#> 55  -0.987

Interpreting Parameters

Discriminant validity: you want traits correlations to be low, which implies that the traits are different things.
Discriminant validity: you want the methods correlations to be low, which implies that the methods are not exactly the same.

parameterestimates(step1.fit, standardized = T)
#>        lhs op     rhs    est    se       z pvalue ci.lower ci.upper std.lv
#> 1      mlq =~      m1  0.072 0.079   0.912  0.362   -0.082    0.226  0.072
#> 2      mlq =~      m2 -1.276 0.071 -17.912  0.000   -1.415   -1.136 -1.276
#> 3      mlq =~      m3 -1.364 0.066 -20.783  0.000   -1.493   -1.236 -1.364
#> 4      mlq =~      m4 -0.011 0.082  -0.133  0.894   -0.171    0.150 -0.011
#> 5      mlq =~      m5  0.044 0.071   0.624  0.533   -0.095    0.183  0.044
#> 6      mlq =~      m6  0.097 0.084   1.146  0.252   -0.069    0.262  0.097
#> 7      mlq =~      m8 -1.332 0.065 -20.402  0.000   -1.460   -1.204 -1.332
#> 8      mlq =~      m9  0.066 0.081   0.813  0.416   -0.093    0.225  0.066
#> 9      mlq =~     m10 -1.302 0.082 -15.838  0.000   -1.463   -1.141 -1.302
#> 10     pil =~      p3  0.708 0.043  16.321  0.000    0.623    0.793  0.708
#> 11     pil =~      p4  0.441 0.041  10.812  0.000    0.361    0.521  0.441
#> 12     pil =~      p8  0.463 0.042  10.942  0.000    0.380    0.546  0.463
#> 13     pil =~     p12  0.344 0.063   5.456  0.000    0.220    0.467  0.344
#> 14     pil =~     p17  0.255 0.049   5.236  0.000    0.160    0.351  0.255
#> 15     pil =~     p20  0.628 0.038  16.314  0.000    0.552    0.703  0.628
#> 16 meaning =~      m1 -1.090 0.049 -22.359  0.000   -1.186   -0.995 -1.090
#> 17 meaning =~      m2  0.414 0.111   3.728  0.000    0.196    0.631  0.414
#> 18 meaning =~      m5 -0.987 0.044 -22.682  0.000   -1.072   -0.902 -0.987
#> 19 meaning =~     m10  0.745 0.115   6.503  0.000    0.520    0.969  0.745
#> 20 meaning =~      p4 -0.658 0.042 -15.527  0.000   -0.741   -0.575 -0.658
#> 21 meaning =~     p12 -0.824 0.061 -13.569  0.000   -0.943   -0.705 -0.824
#> 22 meaning =~     p17 -0.609 0.047 -13.032  0.000   -0.701   -0.517 -0.609
#> 23 purpose =~      m3 -0.157 0.115  -1.369  0.171   -0.382    0.068 -0.157
#> 24 purpose =~      m4  1.149 0.048  23.832  0.000    1.055    1.244  1.149
#> 25 purpose =~      m6  1.147 0.052  21.965  0.000    1.045    1.249  1.147
#> 26 purpose =~      m8 -0.273 0.112  -2.435  0.015   -0.492   -0.053 -0.273
#> 27 purpose =~      m9  0.980 0.057  17.147  0.000    0.868    1.092  0.980
#> 28 purpose =~      p3  0.486 0.045  10.692  0.000    0.397    0.575  0.486
#> 29 purpose =~      p8  0.441 0.042  10.443  0.000    0.359    0.524  0.441
#> 30 purpose =~     p20  0.693 0.043  16.270  0.000    0.609    0.776  0.693
#> 31     mlq ~~ meaning  0.000 0.000      NA     NA    0.000    0.000  0.000
#> 32     pil ~~ meaning  0.000 0.000      NA     NA    0.000    0.000  0.000
#> 33     mlq ~~ purpose  0.000 0.000      NA     NA    0.000    0.000  0.000
#> 34     pil ~~ purpose  0.000 0.000      NA     NA    0.000    0.000  0.000
#> 35      m1 ~~      m1  0.635 0.048  13.361  0.000    0.542    0.728  0.635
#> 36      m2 ~~      m2  1.316 0.100  13.204  0.000    1.121    1.512  1.316
#> 37      m3 ~~      m3  1.089 0.094  11.580  0.000    0.905    1.274  1.089
#> 38      m4 ~~      m4  0.553 0.045  12.200  0.000    0.464    0.642  0.553
#> 39      m5 ~~      m5  0.498 0.038  13.148  0.000    0.424    0.572  0.498
#> 40      m6 ~~      m6  0.743 0.055  13.632  0.000    0.636    0.850  0.743
#> 41      m8 ~~      m8  1.015 0.088  11.561  0.000    0.843    1.187  1.015
#> 42      m9 ~~      m9  1.208 0.078  15.433  0.000    1.054    1.361  1.208
#> 43     m10 ~~     m10  1.352 0.104  13.050  0.000    1.149    1.556  1.352
#> 44      p3 ~~      p3  0.411 0.041   9.997  0.000    0.331    0.492  0.411
#> 45      p4 ~~      p4  0.511 0.035  14.556  0.000    0.443    0.580  0.511
#> 46      p8 ~~      p8  0.592 0.039  15.029  0.000    0.515    0.670  0.592
#> 47     p12 ~~     p12  1.440 0.090  16.075  0.000    1.264    1.615  1.440
#> 48     p17 ~~     p17  0.872 0.054  16.150  0.000    0.766    0.978  0.872
#> 49     p20 ~~     p20  0.287 0.030   9.490  0.000    0.228    0.346  0.287
#> 50     mlq ~~     mlq  1.000 0.000      NA     NA    1.000    1.000  1.000
#> 51     pil ~~     pil  1.000 0.000      NA     NA    1.000    1.000  1.000
#> 52 meaning ~~ meaning  1.000 0.000      NA     NA    1.000    1.000  1.000
#> 53 purpose ~~ purpose  1.000 0.000      NA     NA    1.000    1.000  1.000
#> 54     mlq ~~     pil  0.147 0.083   1.763  0.078   -0.016    0.310  0.147
#> 55 meaning ~~ purpose -0.987 0.011 -92.538  0.000   -1.008   -0.967 -0.987
#>    std.all
#> 1    0.053
#> 2   -0.723
#> 3   -0.791
#> 4   -0.008
#> 5    0.036
#> 6    0.067
#> 7   -0.787
#> 8    0.045
#> 9   -0.686
#> 10   0.660
#> 11   0.413
#> 12   0.463
#> 13   0.230
#> 14   0.223
#> 15   0.583
#> 16  -0.806
#> 17   0.234
#> 18  -0.813
#> 19   0.392
#> 20  -0.617
#> 21  -0.551
#> 22  -0.532
#> 23  -0.091
#> 24   0.839
#> 25   0.798
#> 26  -0.161
#> 27   0.665
#> 28   0.453
#> 29   0.441
#> 30   0.643
#> 31   0.000
#> 32   0.000
#> 33   0.000
#> 34   0.000
#> 35   0.347
#> 36   0.423
#> 37   0.366
#> 38   0.295
#> 39   0.338
#> 40   0.359
#> 41   0.355
#> 42   0.556
#> 43   0.375
#> 44   0.358
#> 45   0.449
#> 46   0.591
#> 47   0.644
#> 48   0.667
#> 49   0.247
#> 50   1.000
#> 51   1.000
#> 52   1.000
#> 53   1.000
#> 54   0.147
#> 55  -0.987

Summary

In this lecture you’ve learned:
- How to examine for confirmatory and discriminant validity using multi-trait multi-method analysis.
- How to examine parameter estimates for confirmation of the model findings.
- How to compare models.
- How to add cross-loadings set to zero and one.