Skip to contents

Data Screening

lecture_data_screen.Rmd

Data Screening Overview

  • In this lecture, we will give you demonstration of what you might do to data screen a dataset for structural equation modeling.

  • There are four key steps:

    • Accuracy: dealing with errors
    • Missing: dealing with missing data
    • Outliers: determining if there are outliers and what to do with them
    • Assumptions: additivity, multivariate normality, linearity, homogeneity, and homoscedasticity

  • Note that the type of data screening may change depending on the type of data you have (i.e., ordinal data has different assumptions)

  • Mostly, we will focus on datasets with traditional parametric assumptions

Hypothesis Testing versus Data Screening

  • Generally, we set an alphaalpha value, or Type 1 error
  • Often, this translates to “statistical significance”, p < alphaalpha = significant, where alphaalpha is often defined as .05
  • In data screening, we want things to be very unusual before correcting or eliminating things
  • Therefore, we will often lower our criterion and use p < alphaalpha to denote problems with the data, where alphaalpha is lowered to .001

Order is Important

  • While datascreening can be performed many ways, it’s important to know that you should fix errors, missing data, etc. before checking assumptions
  • The changes you make effect the next steps

An Example

  • We will learn about data screening by working an example
  • This data is made up data where people were asked to judge their own learning in different experimental conditions, and they rated their confidence of remembering information, and then we measured their actual memory of a situation

Import the Data 

library(rio)
master <- import("data/lecture_data_screen.csv")
names(master)
#>  [1] "JOL_group" "type_cue"  "conf1"     "conf2"     "conf3"     "conf4"    
#>  [7] "conf5"     "conf6"     "conf7"     "conf8"     "conf9"     "conf10"   
#> [13] "rec1"      "rec2"      "rec3"      "rec4"      "rec5"      "rec6"     
#> [19] "rec7"      "rec8"      "rec9"      "rec10"

Accuracy

  • Use the summary() and table() functions to examine the dataset.
  • Categorical data: Are the labels right? Should this variable be factored?
  • Continuous data: is the min/max of the data correct? Are the data scored correctly?

Accuracy Categorical 

#summary(master)
table(master$JOL_group)
#> 
#>   delayed immediate 
#>        84        74

table(master$type_cue)
#> 
#>       cue only stimulus pairs 
#>             76             82

Accuracy Categorical 

no_typos <- master
no_typos$JOL_group <- factor(no_typos$JOL_group,
                             levels = c("delayed", "immediate"),
                             labels = c("Delayed", "Immediate"))

no_typos$type_cue <- factor(no_typos$type_cue, 
                            levels = c("cue only", "stimulus pairs"),
                            labels = c("Cue Only", "Stimulus Pairs"))

Accuracy Continuous

  • Confidence and recall should only be between 0 and 100.
  • Looks like we have some data to clean up.
summary(no_typos)
#>      JOL_group            type_cue      conf1           conf2      
#>  Delayed  :84   Cue Only      :76   Min.   :20.70   Min.   :23.85  
#>  Immediate:74   Stimulus Pairs:82   1st Qu.:42.79   1st Qu.:41.94  
#>                                     Median :49.48   Median :50.63  
#>                                     Mean   :49.28   Mean   :50.29  
#>                                     3rd Qu.:55.50   3rd Qu.:57.21  
#>                                     Max.   :72.40   Max.   :75.42  
#>                                                     NA's   :3      
#>      conf3           conf4            conf5           conf6      
#>  Min.   :24.43   Min.   :-48.75   Min.   :19.97   Min.   :22.31  
#>  1st Qu.:44.41   1st Qu.: 42.04   1st Qu.:43.48   1st Qu.:43.03  
#>  Median :48.94   Median : 48.40   Median :50.79   Median :51.12  
#>  Mean   :49.53   Mean   : 48.24   Mean   :50.91   Mean   :50.67  
#>  3rd Qu.:54.91   3rd Qu.: 55.58   3rd Qu.:57.29   3rd Qu.:57.93  
#>  Max.   :74.27   Max.   : 76.62   Max.   :77.40   Max.   :79.93  
#>  NA's   :3       NA's   :2        NA's   :3       NA's   :4      
#>      conf7           conf8           conf9           conf10      
#>  Min.   :22.15   Min.   :24.74   Min.   :25.16   Min.   : 25.87  
#>  1st Qu.:43.59   1st Qu.:42.81   1st Qu.:41.48   1st Qu.: 43.13  
#>  Median :48.51   Median :50.75   Median :50.66   Median : 49.10  
#>  Mean   :49.55   Mean   :50.61   Mean   :49.61   Mean   : 52.42  
#>  3rd Qu.:56.32   3rd Qu.:58.10   3rd Qu.:56.68   3rd Qu.: 55.79  
#>  Max.   :76.23   Max.   :80.01   Max.   :81.59   Max.   :470.53  
#>  NA's   :5       NA's   :4       NA's   :4       NA's   :4       
#>       rec1            rec2            rec3            rec4      
#>  Min.   :47.39   Min.   :47.91   Min.   :46.79   Min.   :48.35  
#>  1st Qu.:57.33   1st Qu.:55.79   1st Qu.:56.32   1st Qu.:56.51  
#>  Median :60.48   Median :59.95   Median :60.16   Median :59.45  
#>  Mean   :60.25   Mean   :59.90   Mean   :59.85   Mean   :59.74  
#>  3rd Qu.:63.50   3rd Qu.:63.58   3rd Qu.:63.56   3rd Qu.:62.87  
#>  Max.   :71.60   Max.   :71.43   Max.   :72.08   Max.   :74.07  
#>  NA's   :3       NA's   :3       NA's   :3       NA's   :3      
#>       rec5             rec6             rec7            rec8      
#>  Min.   :-59.85   Min.   : 42.84   Min.   :46.67   Min.   :50.64  
#>  1st Qu.: 56.31   1st Qu.: 56.96   1st Qu.:56.88   1st Qu.:56.58  
#>  Median : 59.33   Median : 60.19   Median :60.15   Median :59.16  
#>  Mean   : 58.84   Mean   : 60.81   Mean   :60.17   Mean   :59.62  
#>  3rd Qu.: 62.72   3rd Qu.: 63.84   3rd Qu.:64.18   3rd Qu.:62.64  
#>  Max.   : 73.07   Max.   :161.86   Max.   :71.01   Max.   :72.50  
#>  NA's   :5        NA's   :3        NA's   :4       NA's   :3      
#>       rec9           rec10      
#>  Min.   :45.66   Min.   :45.49  
#>  1st Qu.:56.04   1st Qu.:56.17  
#>  Median :59.40   Median :59.68  
#>  Mean   :59.56   Mean   :59.47  
#>  3rd Qu.:63.12   3rd Qu.:62.70  
#>  Max.   :73.32   Max.   :72.59  
#>  NA's   :4       NA's   :3

Accuracy Continuous 

# how did I get 3:22?
# how did I get the rule?
# what should I do? 
no_typos[ , 3:22][ no_typos[ , 3:22] > 100 ]
#>  [1]       NA       NA       NA       NA       NA       NA       NA       NA
#>  [9]       NA       NA       NA       NA       NA       NA       NA       NA
#> [17]       NA       NA       NA       NA       NA       NA       NA       NA
#> [25]       NA       NA       NA       NA       NA       NA 470.5320       NA
#> [33]       NA       NA       NA       NA       NA       NA       NA       NA
#> [41]       NA       NA       NA       NA       NA       NA       NA       NA
#> [49]       NA       NA       NA 161.8596       NA       NA       NA       NA
#> [57]       NA       NA       NA       NA       NA       NA       NA       NA
#> [65]       NA       NA       NA       NA

no_typos[ , 3:22][ no_typos[ , 3:22] > 100 ] <- NA

no_typos[ , 3:22][ no_typos[ , 3:22] < 0 ] <- NA

Missing

  • There are two main types of missing data:

    • Missing not at random: when data is missing because of a common cause (i.e., everyone skipped question five)
    • Missing completely at random: data is randomly missing, potentially due to computer or human error

  • We also have to distinguish between missing data and incomplete data

no_missing <- no_typos
summary(no_missing)
#>      JOL_group            type_cue      conf1           conf2      
#>  Delayed  :84   Cue Only      :76   Min.   :20.70   Min.   :23.85  
#>  Immediate:74   Stimulus Pairs:82   1st Qu.:42.79   1st Qu.:41.94  
#>                                     Median :49.48   Median :50.63  
#>                                     Mean   :49.28   Mean   :50.29  
#>                                     3rd Qu.:55.50   3rd Qu.:57.21  
#>                                     Max.   :72.40   Max.   :75.42  
#>                                                     NA's   :3      
#>      conf3           conf4           conf5           conf6      
#>  Min.   :24.43   Min.   :20.92   Min.   :19.97   Min.   :22.31  
#>  1st Qu.:44.41   1st Qu.:42.12   1st Qu.:43.48   1st Qu.:43.03  
#>  Median :48.94   Median :48.42   Median :50.79   Median :51.12  
#>  Mean   :49.53   Mean   :48.86   Mean   :50.91   Mean   :50.67  
#>  3rd Qu.:54.91   3rd Qu.:55.62   3rd Qu.:57.29   3rd Qu.:57.93  
#>  Max.   :74.27   Max.   :76.62   Max.   :77.40   Max.   :79.93  
#>  NA's   :3       NA's   :3       NA's   :3       NA's   :4      
#>      conf7           conf8           conf9           conf10     
#>  Min.   :22.15   Min.   :24.74   Min.   :25.16   Min.   :25.87  
#>  1st Qu.:43.59   1st Qu.:42.81   1st Qu.:41.48   1st Qu.:43.07  
#>  Median :48.51   Median :50.75   Median :50.66   Median :49.00  
#>  Mean   :49.55   Mean   :50.61   Mean   :49.61   Mean   :49.69  
#>  3rd Qu.:56.32   3rd Qu.:58.10   3rd Qu.:56.68   3rd Qu.:55.77  
#>  Max.   :76.23   Max.   :80.01   Max.   :81.59   Max.   :78.00  
#>  NA's   :5       NA's   :4       NA's   :4       NA's   :5      
#>       rec1            rec2            rec3            rec4      
#>  Min.   :47.39   Min.   :47.91   Min.   :46.79   Min.   :48.35  
#>  1st Qu.:57.33   1st Qu.:55.79   1st Qu.:56.32   1st Qu.:56.51  
#>  Median :60.48   Median :59.95   Median :60.16   Median :59.45  
#>  Mean   :60.25   Mean   :59.90   Mean   :59.85   Mean   :59.74  
#>  3rd Qu.:63.50   3rd Qu.:63.58   3rd Qu.:63.56   3rd Qu.:62.87  
#>  Max.   :71.60   Max.   :71.43   Max.   :72.08   Max.   :74.07  
#>  NA's   :3       NA's   :3       NA's   :3       NA's   :3      
#>       rec5            rec6            rec7            rec8      
#>  Min.   :48.28   Min.   :42.84   Min.   :46.67   Min.   :50.64  
#>  1st Qu.:56.40   1st Qu.:56.95   1st Qu.:56.88   1st Qu.:56.58  
#>  Median :59.35   Median :60.15   Median :60.15   Median :59.16  
#>  Mean   :59.62   Mean   :60.16   Mean   :60.17   Mean   :59.62  
#>  3rd Qu.:62.74   3rd Qu.:63.78   3rd Qu.:64.18   3rd Qu.:62.64  
#>  Max.   :73.07   Max.   :71.56   Max.   :71.01   Max.   :72.50  
#>  NA's   :6       NA's   :4       NA's   :4       NA's   :3      
#>       rec9           rec10      
#>  Min.   :45.66   Min.   :45.49  
#>  1st Qu.:56.04   1st Qu.:56.17  
#>  Median :59.40   Median :59.68  
#>  Mean   :59.56   Mean   :59.47  
#>  3rd Qu.:63.12   3rd Qu.:62.70  
#>  Max.   :73.32   Max.   :72.59  
#>  NA's   :4       NA's   :3

Missing Rows 

percent_missing <- function(x){sum(is.na(x))/length(x) * 100}
missing <- apply(no_missing, 1, percent_missing)
table(missing)
#> missing
#>                0 4.54545454545455 27.2727272727273 68.1818181818182 
#>              139               15                1                2 
#> 86.3636363636364 
#>                1

Missing Replacement

  • How much data can I safely replace?

    • Replace only things that make sense.
    • Replace as minimal as possible, often less than 5%
    • Replace based on completion/missingness type
replace_rows <- subset(no_missing, missing <= 5)
no_rows <- subset(no_missing, missing > 5)

Missing Columns

  • Separate out columns that you should not replace
  • Make sure columns have less than 5% missing for replacement
missing <- apply(replace_rows, 2, percent_missing)
table(missing)
#> missing
#>                 0 0.649350649350649   1.2987012987013  1.94805194805195 
#>                12                 6                 3                 1

replace_columns <- replace_rows[ , 3:22]
no_columns <- replace_rows[ , 1:2]

Missing Replacement 

library(mice)
#> 
#> Attaching package: 'mice'
#> The following object is masked from 'package:stats':
#> 
#>     filter
#> The following objects are masked from 'package:base':
#> 
#>     cbind, rbind
tempnomiss <- mice(replace_columns)
#> 
#>  iter imp variable
#>   1   1  conf2  conf3  conf4  conf5  conf7  conf10  rec5  rec6  rec7  rec9
#>   1   2  conf2  conf3  conf4  conf5  conf7  conf10  rec5  rec6  rec7  rec9
#>   1   3  conf2  conf3  conf4  conf5  conf7  conf10  rec5  rec6  rec7  rec9
#>   1   4  conf2  conf3  conf4  conf5  conf7  conf10  rec5  rec6  rec7  rec9
#>   1   5  conf2  conf3  conf4  conf5  conf7  conf10  rec5  rec6  rec7  rec9
#>   2   1  conf2  conf3  conf4  conf5  conf7  conf10  rec5  rec6  rec7  rec9
#>   2   2  conf2  conf3  conf4  conf5  conf7  conf10  rec5  rec6  rec7  rec9
#>   2   3  conf2  conf3  conf4  conf5  conf7  conf10  rec5  rec6  rec7  rec9
#>   2   4  conf2  conf3  conf4  conf5  conf7  conf10  rec5  rec6  rec7  rec9
#>   2   5  conf2  conf3  conf4  conf5  conf7  conf10  rec5  rec6  rec7  rec9
#>   3   1  conf2  conf3  conf4  conf5  conf7  conf10  rec5  rec6  rec7  rec9
#>   3   2  conf2  conf3  conf4  conf5  conf7  conf10  rec5  rec6  rec7  rec9
#>   3   3  conf2  conf3  conf4  conf5  conf7  conf10  rec5  rec6  rec7  rec9
#>   3   4  conf2  conf3  conf4  conf5  conf7  conf10  rec5  rec6  rec7  rec9
#>   3   5  conf2  conf3  conf4  conf5  conf7  conf10  rec5  rec6  rec7  rec9
#>   4   1  conf2  conf3  conf4  conf5  conf7  conf10  rec5  rec6  rec7  rec9
#>   4   2  conf2  conf3  conf4  conf5  conf7  conf10  rec5  rec6  rec7  rec9
#>   4   3  conf2  conf3  conf4  conf5  conf7  conf10  rec5  rec6  rec7  rec9
#>   4   4  conf2  conf3  conf4  conf5  conf7  conf10  rec5  rec6  rec7  rec9
#>   4   5  conf2  conf3  conf4  conf5  conf7  conf10  rec5  rec6  rec7  rec9
#>   5   1  conf2  conf3  conf4  conf5  conf7  conf10  rec5  rec6  rec7  rec9
#>   5   2  conf2  conf3  conf4  conf5  conf7  conf10  rec5  rec6  rec7  rec9
#>   5   3  conf2  conf3  conf4  conf5  conf7  conf10  rec5  rec6  rec7  rec9
#>   5   4  conf2  conf3  conf4  conf5  conf7  conf10  rec5  rec6  rec7  rec9
#>   5   5  conf2  conf3  conf4  conf5  conf7  conf10  rec5  rec6  rec7  rec9

Missing Put Together 

fixed_columns <- complete(tempnomiss)
all_columns <- cbind(no_columns, fixed_columns)
all_rows <- rbind(all_columns, no_rows)
nrow(no_missing)
#> [1] 158
nrow(all_rows)
#> [1] 158

Outliers

  • We will mostly be concerned with multivariate outliers in SEM.

  • These are rows of data (participants) who have extremely weird patterns of scores when compared to everyone else.

  • We will use Mahalanobis Distance to examine each row to determine if they are an outlier

    • This score D is the distance from the centriod or mean of means
    • We will use a cutoff score based on our strict screening criterion, p < .001 to determine if they are an outlier
    • This cutoff criterion is based on the number of variables rather than the number of observations

Outliers Mahalanobis 

mahal <- mahalanobis(all_columns[ , -c(1,2)], #take note here 
  colMeans(all_columns[ , -c(1,2)], na.rm=TRUE),
  cov(all_columns[ , -c(1,2)], use ="pairwise.complete.obs"))

cutoff <- qchisq(p = 1 - .001, #1 minus alpha
                 df = ncol(all_columns[ , -c(1,2)])) # number of columns

Outliers Mahalanobis

  • Do outliers really matter in a SEM analysis though?
cutoff
#> [1] 45.31475

summary(mahal < cutoff) #notice the direction 
#>    Mode    TRUE 
#> logical     154

no_outliers <- subset(all_columns, mahal < cutoff)

Assumptions Additivity

  • Additivity is the assumption that each variable adds something to the model
  • You basically do not want to use the same variable twice, as that lowers power
  • Often this is described as multicollinearity
  • Mainly, SEM analysis has a lot of correlated variables, you just want to make sure they aren’t perfectly correlated

Assumptions Additivity 

library(corrplot)
#> corrplot 0.95 loaded
corrplot(cor(no_outliers[ , -c(1,2)]))

Assumptions Set Up 

random_variable <- rchisq(nrow(no_outliers), 7)
fake_model <- lm(random_variable ~ ., 
                 data = no_outliers[ , -c(1,2)])
standardized <- rstudent(fake_model)
fitvalues <- scale(fake_model$fitted.values)

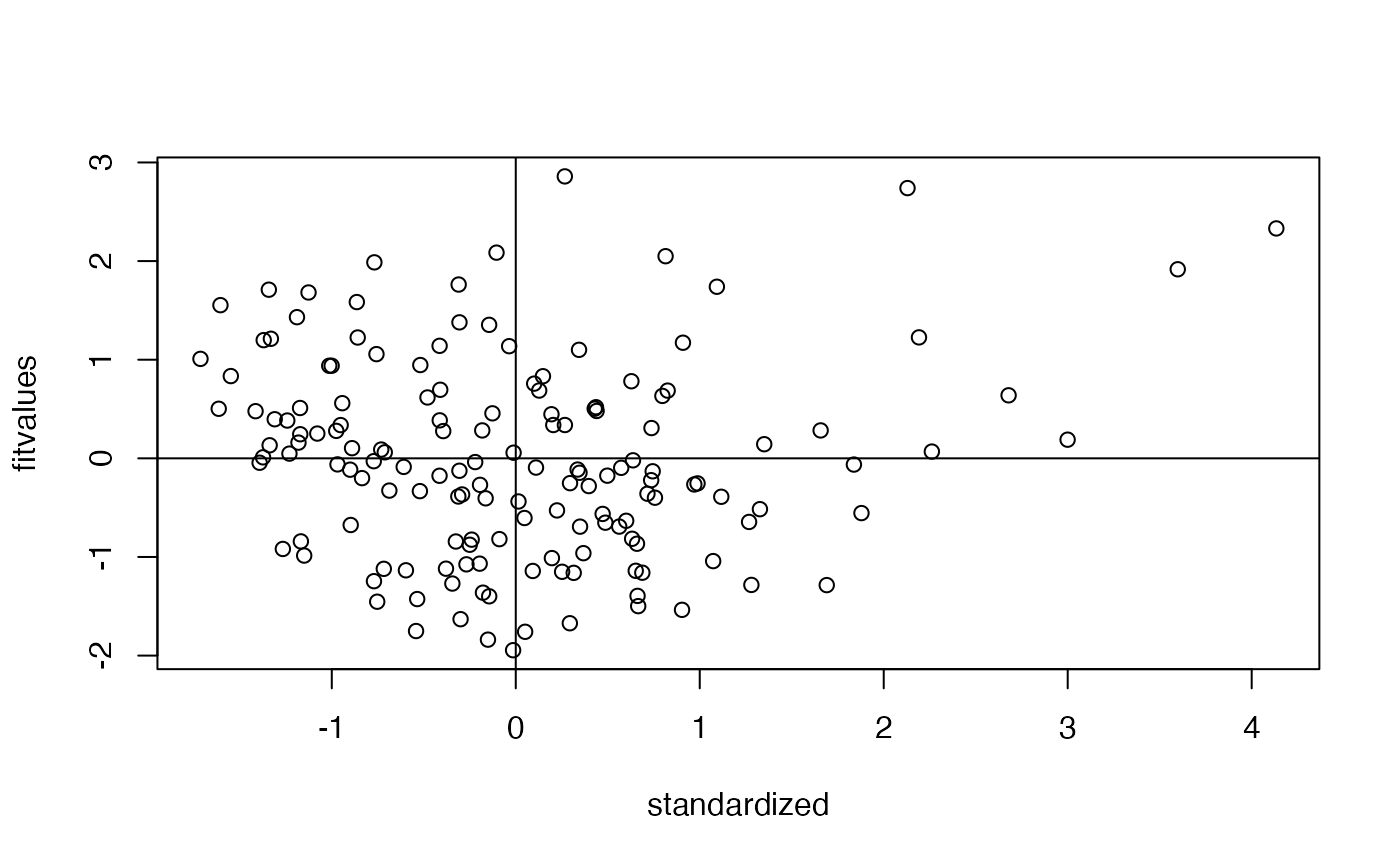
Assumptions Linearity

  • We assume the the multivariate relationship between continuous variables is linear (i.e., no curved)
  • There are many ways to test this, but we can use a QQ/PP Plot to examine for linearity
plot(fake_model, 2)

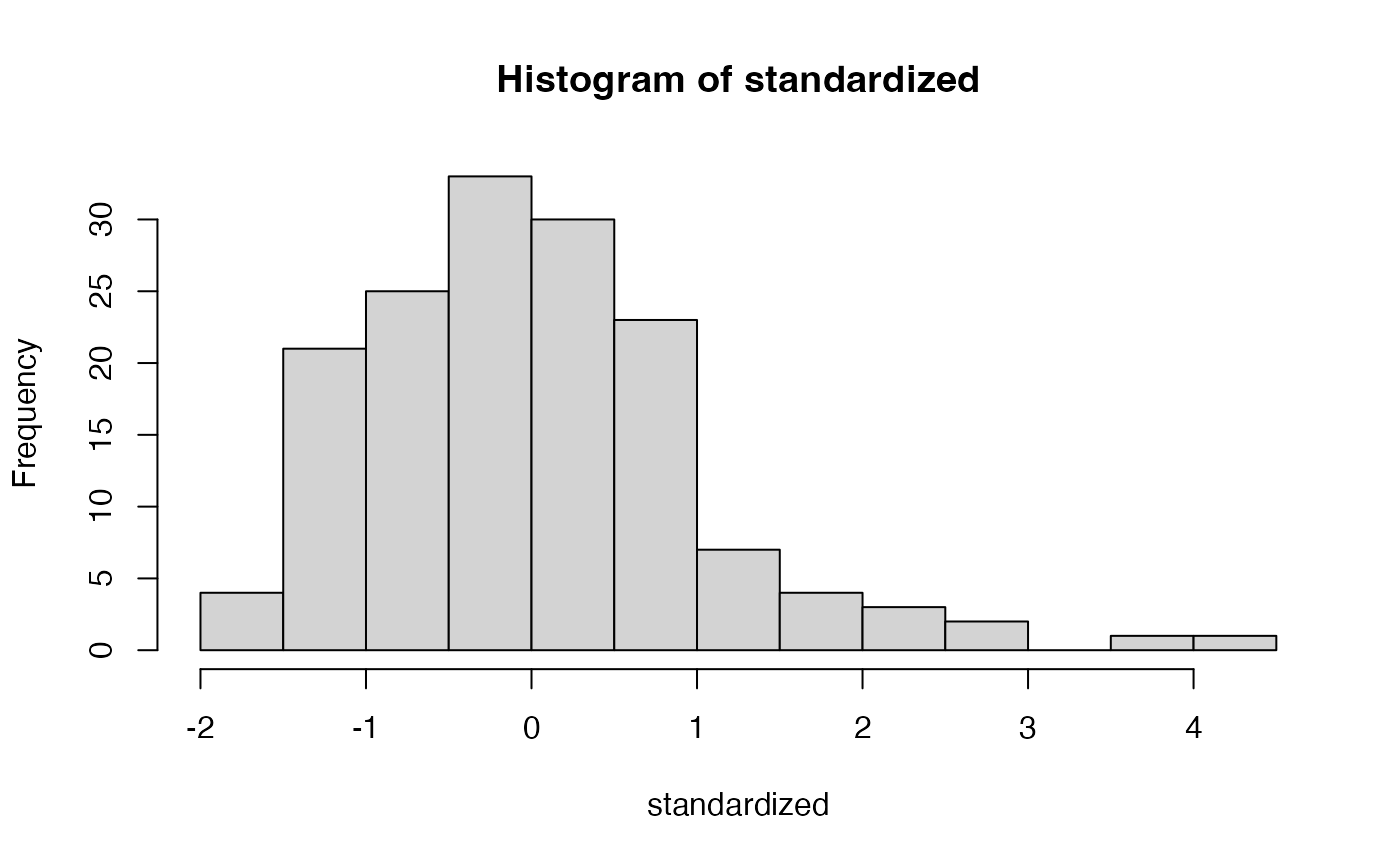
Assumptions Normality

  • We expect that the residuals are normally distributed
  • Not that the sample is normally distributed
  • Generally, SEM requires a large sample size, thus, buffering against normality deviations
hist(standardized)

Assumptions Homogeneity + Homoscedasticity

  • These assumptions are about equality of the variances
  • We assume equal variances between groups for things like t-tests, ANOVA
  • Here the assumption is equality in the spread of variance across predicted values
{plot(standardized, fitvalues)
  abline(v = 0)
  abline(h = 0)
}

Recap

  • We have completed a datascreening check up for our dataset
  • Any problems should be noted, and we will discuss how to handle some of the issues as relevant to SEM analysis
  • Let’s check out the assignment!