Latent Growth Models
lecture_lgm.RmdLatent Growth Modeling
- Measuring change over repeated time measurements
- Gives you more information than a traditional repeated measures ANOVA or regression line by itself.
- Advantages:
- Estimate means and covariances separately
- Estimating observed values and unobserved values separately
Assumptions
- Continuous measurement of the DVs
- This assumption is true for many structural models though!
- Time spacing is the same across people
- NOT across measurements, but people need to be spaced the same
- At least three time points per person (otherwise, you are doing a dependent t-test)
- Large samples!
Before you start
- You have to know the expected type of change before you start
- Generally it’s linear, however, you can do curvilinear or power functions
Example model
- We will set the regression loading values to specific numbers to be able to estimate intercept and slope.
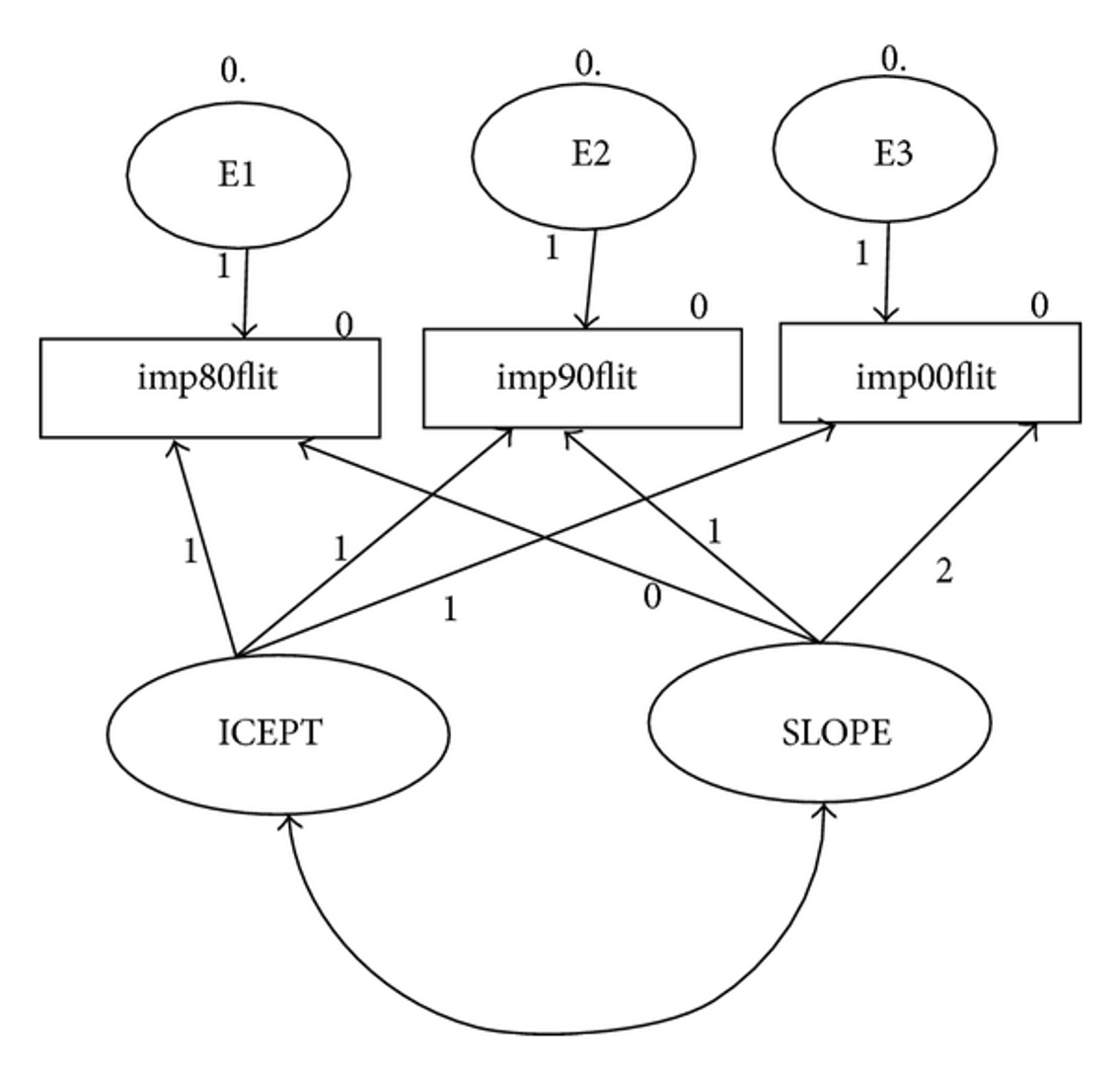
Understand the idea
- Intercept
- You set these values to 1 indicating that you do NOT want to estimate them
- Basically, that gives you a starting value for the first time point, which is the average point where people start (y-intercept)
Understand the idea
- Slope – represents the change over time
- You can set these values to anything you want
- Usually the first time is indicated by a 0
- There’s no slope for time 1, just an intercept
- Then the paths are set based on the time differences between them
Understand the idea
- Setting the parameters this way:
- Helps with identification
- Is theoretical to match the concept of slope and intercept estimation
- Allows you to not have to set the variances, so you can look at them
Questions
- What is the average change for each person?
- Where do they start?
- How does it change over time?
- What is the form of the change?
Questions
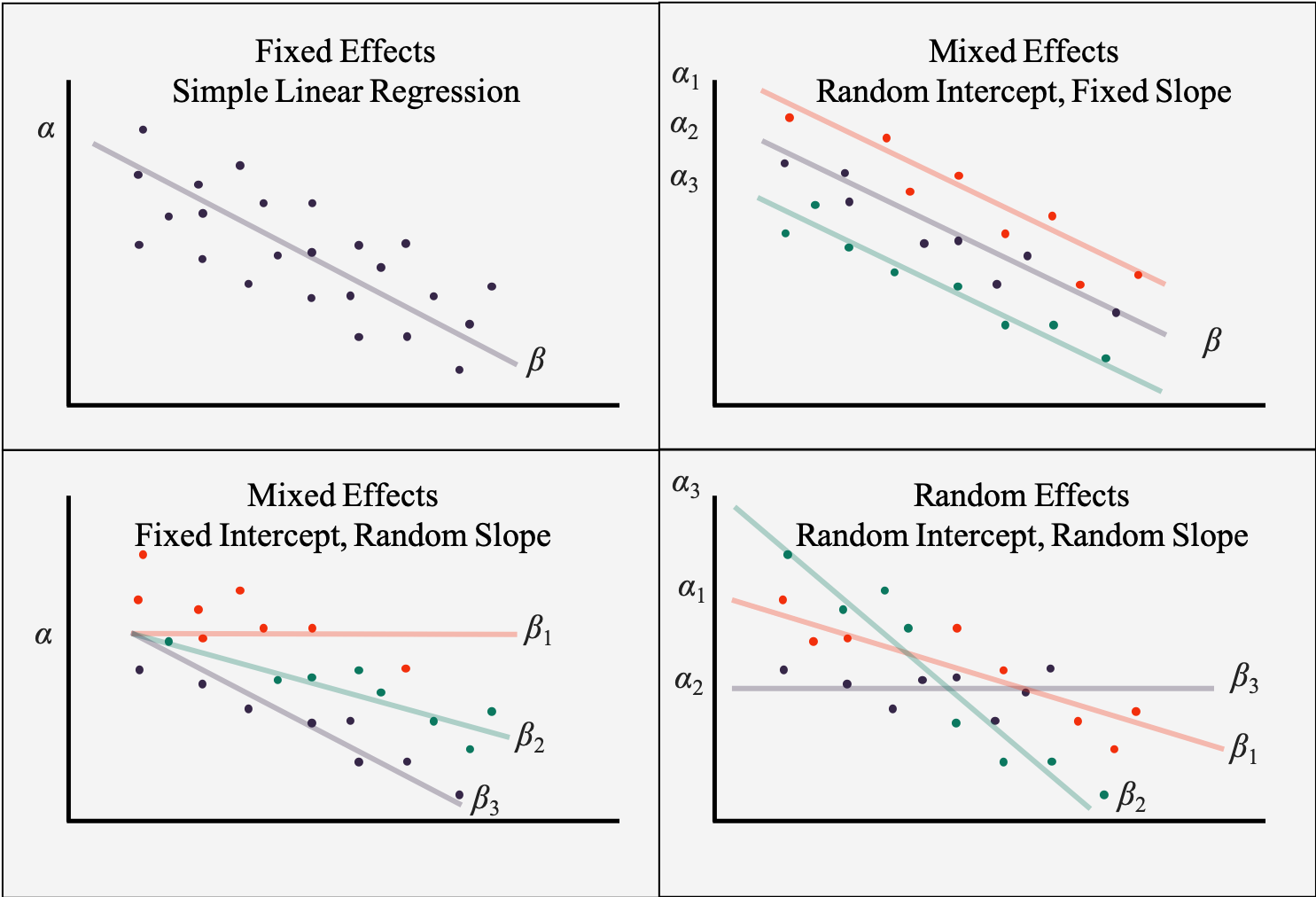
- Is the average slope and intercept a good fit for all participants?
- Or should we include a variance term to account for the differences between people?
- Models are called random effects if you add the random variances (similar to multilevel models)
- If we have a random effects model – is there another variable that explains those random effects?
Understanding the Output
- Intercept mean: the average starting point for time 1
- Slope mean: the average increment across time points
Understanding the Output
- Intercept variance: the spread around the average start point
- Large scores indicate a lot of spread – meaning people start in a lot of different places
- Small scores indicate a small spread – everyone starts about the same place

Understanding the Output
- Slope variance – the range of increments across time points
- Small variances mean that everyone is going up/down about the same amount
- Large variances mean that people scores are going up/down differently (almost like an interaction)

Understanding the Output
- Factor covariance – examines the relationship between intercept and slope
- Positive covariance - positive slope
- People who start with higher intercepts have higher positive slopes
- Positive covariance - negative slope
- People who start higher go down faster (larger negative slopes)
- Negative covariance - positive slope
- People who start with higher intercepts go up slower (smaller slopes)
- Negative covariance - negative slope
- People who start with higher intercepts go down slower
New Functions
-
growth(): This function helps with the set up for a LCM, fixes the parameters correctly for you. - We will use the data as covariances and means, but you can import
the data just like
cfa()
How to Test
- This procedure is very similar to multigroup model testing, only in reverse.
- We are going to start with the most constrained model and slowly let parameters free to see which is the best.
- We would prefer the unconstrained model be the best:
- The slope and intercept are useful
- But the variances to be low indicating everyone has the same pattern of slope and intercept
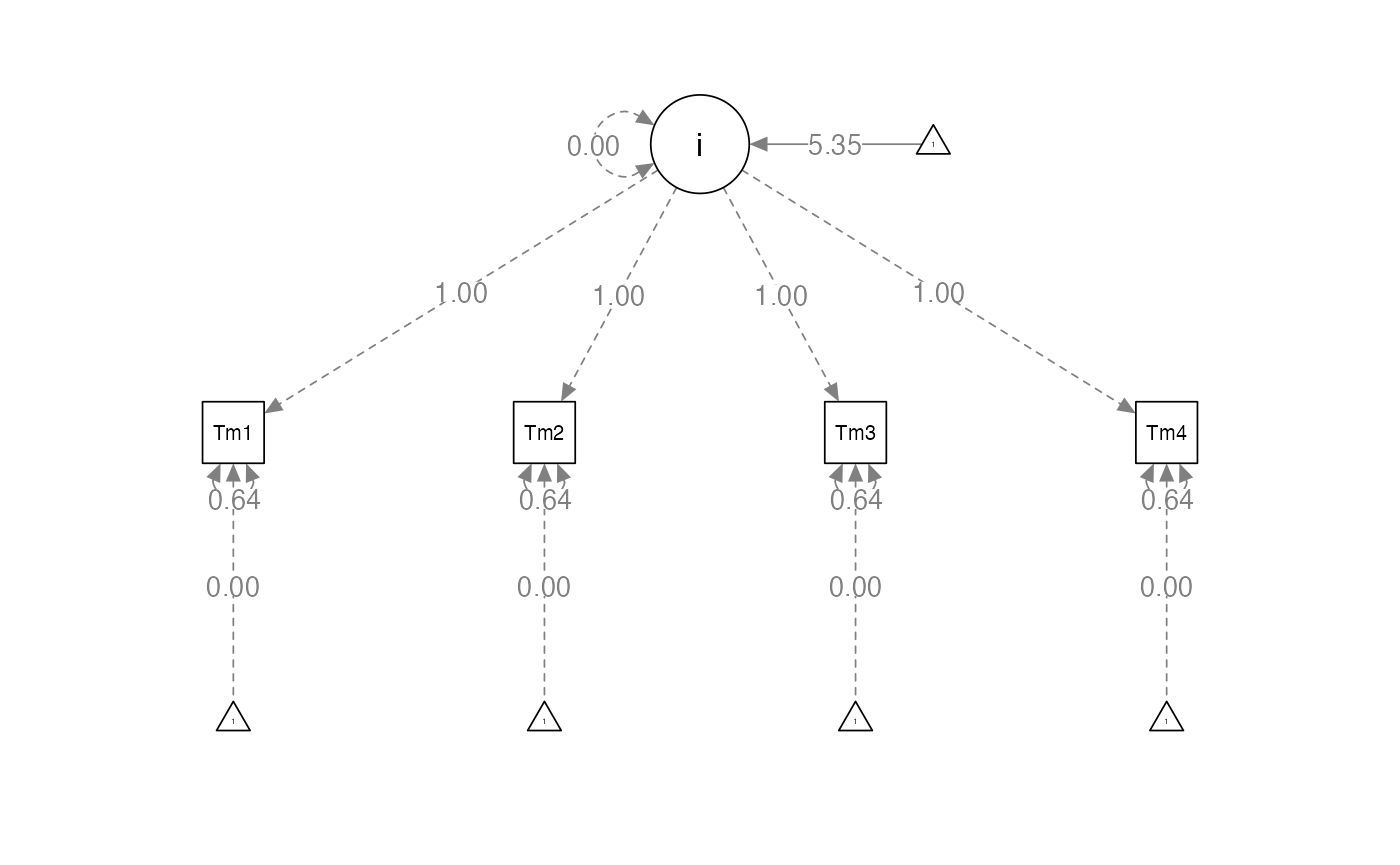
Intercept Only Model
- Use only the intercept (mean of the data) to estimate
- You want this model to be bad, otherwise you are saying that one average score is the best for all the time points
- Intercept variance is constrained to 0, so you only get a mean.
- Residuals are forced to be the same for each time point, so the variance is the same across all time points
crime.model1 <- '
# intercept
i =~ 1*Time1 + 1*Time2 + 1*Time3 + 1*Time4
i~~0*i
# residual variances
Time1~~r*Time1
Time2~~r*Time2
Time3~~r*Time3
Time4~~r*Time4
'Intercept Only Model
crime.fit1 <- growth(crime.model1,
sample.cov=crime.cov,
sample.mean=crime.mean,
sample.nobs=952)
summary(crime.fit1,
standardized = TRUE,
fit.measures = TRUE,
rsquare = TRUE)
#> lavaan 0.6-19 ended normally after 19 iterations
#>
#> Estimator ML
#> Optimization method NLMINB
#> Number of model parameters 5
#> Number of equality constraints 3
#>
#> Number of observations 952
#>
#> Model Test User Model:
#>
#> Test statistic 3461.981
#> Degrees of freedom 12
#> P-value (Chi-square) 0.000
#>
#> Model Test Baseline Model:
#>
#> Test statistic 3358.206
#> Degrees of freedom 6
#> P-value 0.000
#>
#> User Model versus Baseline Model:
#>
#> Comparative Fit Index (CFI) 0.000
#> Tucker-Lewis Index (TLI) 0.485
#>
#> Loglikelihood and Information Criteria:
#>
#> Loglikelihood user model (H0) -4540.205
#> Loglikelihood unrestricted model (H1) -2809.215
#>
#> Akaike (AIC) 9084.410
#> Bayesian (BIC) 9094.127
#> Sample-size adjusted Bayesian (SABIC) 9087.775
#>
#> Root Mean Square Error of Approximation:
#>
#> RMSEA 0.550
#> 90 Percent confidence interval - lower 0.534
#> 90 Percent confidence interval - upper 0.565
#> P-value H_0: RMSEA <= 0.050 0.000
#> P-value H_0: RMSEA >= 0.080 1.000
#>
#> Standardized Root Mean Square Residual:
#>
#> SRMR 0.523
#>
#> Parameter Estimates:
#>
#> Standard errors Standard
#> Information Expected
#> Information saturated (h1) model Structured
#>
#> Latent Variables:
#> Estimate Std.Err z-value P(>|z|) Std.lv Std.all
#> i =~
#> Time1 1.000 0.000 0.000
#> Time2 1.000 0.000 0.000
#> Time3 1.000 0.000 0.000
#> Time4 1.000 0.000 0.000
#>
#> Intercepts:
#> Estimate Std.Err z-value P(>|z|) Std.lv Std.all
#> i 5.352 0.013 414.325 0.000 Inf Inf
#>
#> Variances:
#> Estimate Std.Err z-value P(>|z|) Std.lv Std.all
#> i 0.000 NaN NaN
#> .Time1 (r) 0.636 0.015 43.635 0.000 0.636 1.000
#> .Time2 (r) 0.636 0.015 43.635 0.000 0.636 1.000
#> .Time3 (r) 0.636 0.015 43.635 0.000 0.636 1.000
#> .Time4 (r) 0.636 0.015 43.635 0.000 0.636 1.000
#>
#> R-Square:
#> Estimate
#> Time1 0.000
#> Time2 0.000
#> Time3 0.000
#> Time4 0.000Comparison Table Fit Indices
library(knitr)
fit.table <- matrix(NA, nrow = 5, ncol = 6)
colnames(fit.table) <- c("Model", "X2", "df", "RMSEA", "SRMR", "CFI")
fit.table[1, ] <- c("Intercept Only", round(fitmeasures(crime.fit1, c("chisq", "df", "rmsea", "srmr", "cfi")),3))
kable(fit.table)| Model | X2 | df | RMSEA | SRMR | CFI |
|---|---|---|---|---|---|
| Intercept Only | 3461.981 | 12 | 0.55 | 0.523 | 0 |
| NA | NA | NA | NA | NA | NA |
| NA | NA | NA | NA | NA | NA |
| NA | NA | NA | NA | NA | NA |
| NA | NA | NA | NA | NA | NA |
Comparison Table Parameters
#save the parameter estimates
crime.fit1.par <- parameterestimates(crime.fit1)
#make table
par.table <- matrix(NA, nrow = 5, ncol = 7)
colnames(par.table) <- c("Model", "Intercept Mean", "Intercept Variance", "Residual Variance", "Slope Mean", "Slope Variance", "Covariance")
#put data in table
par.table[1, ] <- c("Intercept Only",
round(crime.fit1.par$est[crime.fit1.par$lhs == "i" & crime.fit1.par$op == "~1"], 3),
"X",
round(crime.fit1.par$est[crime.fit1.par$lhs == "Time1" & crime.fit1.par$op == "~~"], 3),
"X",
"X",
"X")
kable(par.table)| Model | Intercept Mean | Intercept Variance | Residual Variance | Slope Mean | Slope Variance | Covariance |
|---|---|---|---|---|---|---|
| Intercept Only | 5.352 | X | 0.636 | X | X | X |
| NA | NA | NA | NA | NA | NA | NA |
| NA | NA | NA | NA | NA | NA | NA |
| NA | NA | NA | NA | NA | NA | NA |
| NA | NA | NA | NA | NA | NA | NA |
Random Intercept Only Model
- We allow the intercept variance to be > 0
- People can start at different places
- Residual variances are still the same
- Still no slope
crime.model2 <- '
# intercept
i =~ 1*Time1 + 1*Time2 + 1*Time3 + 1*Time4
# residual variances
Time1~~r*Time1
Time2~~r*Time2
Time3~~r*Time3
Time4~~r*Time4
'Random Intercept Only Model
crime.fit2 <- growth(crime.model2,
sample.cov=crime.cov,
sample.mean=crime.mean,
sample.nobs=952)
summary(crime.fit2,
standardized = TRUE,
fit.measures = TRUE,
rsquare = TRUE)
#> lavaan 0.6-19 ended normally after 19 iterations
#>
#> Estimator ML
#> Optimization method NLMINB
#> Number of model parameters 6
#> Number of equality constraints 3
#>
#> Number of observations 952
#>
#> Model Test User Model:
#>
#> Test statistic 555.313
#> Degrees of freedom 11
#> P-value (Chi-square) 0.000
#>
#> Model Test Baseline Model:
#>
#> Test statistic 3358.206
#> Degrees of freedom 6
#> P-value 0.000
#>
#> User Model versus Baseline Model:
#>
#> Comparative Fit Index (CFI) 0.838
#> Tucker-Lewis Index (TLI) 0.911
#>
#> Loglikelihood and Information Criteria:
#>
#> Loglikelihood user model (H0) -3086.871
#> Loglikelihood unrestricted model (H1) -2809.215
#>
#> Akaike (AIC) 6179.742
#> Bayesian (BIC) 6194.318
#> Sample-size adjusted Bayesian (SABIC) 6184.790
#>
#> Root Mean Square Error of Approximation:
#>
#> RMSEA 0.228
#> 90 Percent confidence interval - lower 0.212
#> 90 Percent confidence interval - upper 0.244
#> P-value H_0: RMSEA <= 0.050 0.000
#> P-value H_0: RMSEA >= 0.080 1.000
#>
#> Standardized Root Mean Square Residual:
#>
#> SRMR 0.092
#>
#> Parameter Estimates:
#>
#> Standard errors Standard
#> Information Expected
#> Information saturated (h1) model Structured
#>
#> Latent Variables:
#> Estimate Std.Err z-value P(>|z|) Std.lv Std.all
#> i =~
#> Time1 1.000 0.693 0.870
#> Time2 1.000 0.693 0.870
#> Time3 1.000 0.693 0.870
#> Time4 1.000 0.693 0.870
#>
#> Intercepts:
#> Estimate Std.Err z-value P(>|z|) Std.lv Std.all
#> i 5.352 0.023 229.140 0.000 7.720 7.720
#>
#> Variances:
#> Estimate Std.Err z-value P(>|z|) Std.lv Std.all
#> .Time1 (r) 0.155 0.004 37.789 0.000 0.155 0.244
#> .Time2 (r) 0.155 0.004 37.789 0.000 0.155 0.244
#> .Time3 (r) 0.155 0.004 37.789 0.000 0.155 0.244
#> .Time4 (r) 0.155 0.004 37.789 0.000 0.155 0.244
#> i 0.481 0.024 20.174 0.000 1.000 1.000
#>
#> R-Square:
#> Estimate
#> Time1 0.756
#> Time2 0.756
#> Time3 0.756
#> Time4 0.756Comparison Table Fit Indices
- This model is much better than model 1
- Implies that people all start in different places
fit.table[2, ] <- c("Random Intercept", round(fitmeasures(crime.fit2, c("chisq", "df", "rmsea", "srmr", "cfi")),3))
kable(fit.table)| Model | X2 | df | RMSEA | SRMR | CFI |
|---|---|---|---|---|---|
| Intercept Only | 3461.981 | 12 | 0.55 | 0.523 | 0 |
| Random Intercept | 555.313 | 11 | 0.228 | 0.092 | 0.838 |
| NA | NA | NA | NA | NA | NA |
| NA | NA | NA | NA | NA | NA |
| NA | NA | NA | NA | NA | NA |
Comparison Table Parameters
#save the parameter estimates
crime.fit2.par <- parameterestimates(crime.fit2)
#put data in table
par.table[2, ] <- c("Random Intercept",
round(crime.fit2.par$est[crime.fit2.par$lhs == "i" & crime.fit2.par$op == "~1"], 3),
round(crime.fit2.par$est[crime.fit2.par$lhs == "i" & crime.fit2.par$op == "~~"], 3),
round(crime.fit2.par$est[crime.fit2.par$lhs == "Time1" & crime.fit2.par$op == "~~"], 3),
"X",
"X",
"X")
kable(par.table)| Model | Intercept Mean | Intercept Variance | Residual Variance | Slope Mean | Slope Variance | Covariance |
|---|---|---|---|---|---|---|
| Intercept Only | 5.352 | X | 0.636 | X | X | X |
| Random Intercept | 5.352 | 0.481 | 0.155 | X | X | X |
| NA | NA | NA | NA | NA | NA | NA |
| NA | NA | NA | NA | NA | NA | NA |
| NA | NA | NA | NA | NA | NA | NA |
Random Slope + Intercepts
- Add in the random slope
-
s~0*1(makes the average slope 0) -
s~~0*i(uncorrelated slope/intercept)
-
- Leave the intercept and its variance in the model
- Keep the residuals constrained to be the same
crime.model3 <- '
# intercept
i =~ 1*Time1 + 1*Time2 + 1*Time3 + 1*Time4
# slope
s =~ 0*Time1 + 1*Time2 + 2*Time3 + 3*Time4
s~0*1
s~~0*i
# residual variances
Time1~~r*Time1
Time2~~r*Time2
Time3~~r*Time3
Time4~~r*Time4
'Random Slope + Intercepts
crime.fit3 <- growth(crime.model3,
sample.cov=crime.cov,
sample.mean=crime.mean,
sample.nobs=952)
summary(crime.fit3,
standardized = TRUE,
fit.measures = TRUE,
rsquare = TRUE)
#> lavaan 0.6-19 ended normally after 38 iterations
#>
#> Estimator ML
#> Optimization method NLMINB
#> Number of model parameters 7
#> Number of equality constraints 3
#>
#> Number of observations 952
#>
#> Model Test User Model:
#>
#> Test statistic 339.586
#> Degrees of freedom 10
#> P-value (Chi-square) 0.000
#>
#> Model Test Baseline Model:
#>
#> Test statistic 3358.206
#> Degrees of freedom 6
#> P-value 0.000
#>
#> User Model versus Baseline Model:
#>
#> Comparative Fit Index (CFI) 0.902
#> Tucker-Lewis Index (TLI) 0.941
#>
#> Loglikelihood and Information Criteria:
#>
#> Loglikelihood user model (H0) -2979.008
#> Loglikelihood unrestricted model (H1) -2809.215
#>
#> Akaike (AIC) 5966.015
#> Bayesian (BIC) 5985.450
#> Sample-size adjusted Bayesian (SABIC) 5972.746
#>
#> Root Mean Square Error of Approximation:
#>
#> RMSEA 0.186
#> 90 Percent confidence interval - lower 0.169
#> 90 Percent confidence interval - upper 0.203
#> P-value H_0: RMSEA <= 0.050 0.000
#> P-value H_0: RMSEA >= 0.080 1.000
#>
#> Standardized Root Mean Square Residual:
#>
#> SRMR 0.149
#>
#> Parameter Estimates:
#>
#> Standard errors Standard
#> Information Expected
#> Information saturated (h1) model Structured
#>
#> Latent Variables:
#> Estimate Std.Err z-value P(>|z|) Std.lv Std.all
#> i =~
#> Time1 1.000 0.696 0.903
#> Time2 1.000 0.696 0.884
#> Time3 1.000 0.696 0.835
#> Time4 1.000 0.696 0.768
#> s =~
#> Time1 0.000 0.000 0.000
#> Time2 1.000 0.158 0.201
#> Time3 2.000 0.317 0.380
#> Time4 3.000 0.475 0.525
#>
#> Covariances:
#> Estimate Std.Err z-value P(>|z|) Std.lv Std.all
#> i ~~
#> s 0.000 0.000 0.000
#>
#> Intercepts:
#> Estimate Std.Err z-value P(>|z|) Std.lv Std.all
#> s 0.000 0.000 0.000
#> i 5.262 0.024 221.401 0.000 7.565 7.565
#>
#> Variances:
#> Estimate Std.Err z-value P(>|z|) Std.lv Std.all
#> .Time1 (r) 0.110 0.003 31.461 0.000 0.110 0.185
#> .Time2 (r) 0.110 0.003 31.461 0.000 0.110 0.178
#> .Time3 (r) 0.110 0.003 31.461 0.000 0.110 0.159
#> .Time4 (r) 0.110 0.003 31.461 0.000 0.110 0.134
#> i 0.484 0.025 19.597 0.000 1.000 1.000
#> s 0.025 0.002 11.651 0.000 1.000 1.000
#>
#> R-Square:
#> Estimate
#> Time1 0.815
#> Time2 0.822
#> Time3 0.841
#> Time4 0.866Comparison Table Fit Indices
- This model is much better than model 2
- Implies that having at least a random slope is better than no slope
fit.table[3, ] <- c("Random Slope", round(fitmeasures(crime.fit3, c("chisq", "df", "rmsea", "srmr", "cfi")),3))
kable(fit.table)| Model | X2 | df | RMSEA | SRMR | CFI |
|---|---|---|---|---|---|
| Intercept Only | 3461.981 | 12 | 0.55 | 0.523 | 0 |
| Random Intercept | 555.313 | 11 | 0.228 | 0.092 | 0.838 |
| Random Slope | 339.586 | 10 | 0.186 | 0.149 | 0.902 |
| NA | NA | NA | NA | NA | NA |
| NA | NA | NA | NA | NA | NA |
Comparison Table Parameters
#save the parameter estimates
crime.fit3.par <- parameterestimates(crime.fit3)
#put data in table
par.table[3, ] <- c("Random Slope",
round(crime.fit3.par$est[crime.fit3.par$lhs == "i" & crime.fit3.par$op == "~1"], 3),
round(crime.fit3.par$est[crime.fit3.par$lhs == "i" & crime.fit3.par$op == "~~" & crime.fit3.par$rhs == "i"], 3),
round(crime.fit3.par$est[crime.fit3.par$lhs == "Time1" & crime.fit3.par$op == "~~"], 3),
"X",
round(crime.fit3.par$est[crime.fit3.par$lhs == "s" & crime.fit3.par$op == "~~"], 3),
"X")
kable(par.table)| Model | Intercept Mean | Intercept Variance | Residual Variance | Slope Mean | Slope Variance | Covariance |
|---|---|---|---|---|---|---|
| Intercept Only | 5.352 | X | 0.636 | X | X | X |
| Random Intercept | 5.352 | 0.481 | 0.155 | X | X | X |
| Random Slope | 5.262 | 0.484 | 0.11 | X | 0.025 | X |
| NA | NA | NA | NA | NA | NA | NA |
| NA | NA | NA | NA | NA | NA | NA |
Full Slopes + Intercept
- Allow the slope and intercept to vary
- Constrain the residual variances
crime.model4 <- '
# intercept
i =~ 1*Time1 + 1*Time2 + 1*Time3 + 1*Time4
# slope
s =~ 0*Time1 + 1*Time2 + 2*Time3 + 3*Time4
# residual variances
Time1~~r*Time1
Time2~~r*Time2
Time3~~r*Time3
Time4~~r*Time4
'Full Slopes + Intercept
- Significant covariance – negative covariance with positive slope
- People who start high go up slower than people who start lower.
crime.fit4 <- growth(crime.model4,
sample.cov=crime.cov,
sample.mean=crime.mean,
sample.nobs=952)
summary(crime.fit4,
standardized = TRUE,
fit.measures = TRUE,
rsquare = TRUE)
#> lavaan 0.6-19 ended normally after 33 iterations
#>
#> Estimator ML
#> Optimization method NLMINB
#> Number of model parameters 9
#> Number of equality constraints 3
#>
#> Number of observations 952
#>
#> Model Test User Model:
#>
#> Test statistic 24.001
#> Degrees of freedom 8
#> P-value (Chi-square) 0.002
#>
#> Model Test Baseline Model:
#>
#> Test statistic 3358.206
#> Degrees of freedom 6
#> P-value 0.000
#>
#> User Model versus Baseline Model:
#>
#> Comparative Fit Index (CFI) 0.995
#> Tucker-Lewis Index (TLI) 0.996
#>
#> Loglikelihood and Information Criteria:
#>
#> Loglikelihood user model (H0) -2821.215
#> Loglikelihood unrestricted model (H1) -2809.215
#>
#> Akaike (AIC) 5654.431
#> Bayesian (BIC) 5683.582
#> Sample-size adjusted Bayesian (SABIC) 5664.526
#>
#> Root Mean Square Error of Approximation:
#>
#> RMSEA 0.046
#> 90 Percent confidence interval - lower 0.025
#> 90 Percent confidence interval - upper 0.067
#> P-value H_0: RMSEA <= 0.050 0.589
#> P-value H_0: RMSEA >= 0.080 0.004
#>
#> Standardized Root Mean Square Residual:
#>
#> SRMR 0.020
#>
#> Parameter Estimates:
#>
#> Standard errors Standard
#> Information Expected
#> Information saturated (h1) model Structured
#>
#> Latent Variables:
#> Estimate Std.Err z-value P(>|z|) Std.lv Std.all
#> i =~
#> Time1 1.000 0.720 0.911
#> Time2 1.000 0.720 0.930
#> Time3 1.000 0.720 0.925
#> Time4 1.000 0.720 0.896
#> s =~
#> Time1 0.000 0.000 0.000
#> Time2 1.000 0.128 0.165
#> Time3 2.000 0.255 0.328
#> Time4 3.000 0.383 0.476
#>
#> Covariances:
#> Estimate Std.Err z-value P(>|z|) Std.lv Std.all
#> i ~~
#> s -0.021 0.005 -4.002 0.000 -0.228 -0.228
#>
#> Intercepts:
#> Estimate Std.Err z-value P(>|z|) Std.lv Std.all
#> i 5.183 0.025 207.586 0.000 7.194 7.194
#> s 0.113 0.006 17.990 0.000 0.885 0.885
#>
#> Variances:
#> Estimate Std.Err z-value P(>|z|) Std.lv Std.all
#> .Time1 (r) 0.106 0.003 30.854 0.000 0.106 0.170
#> .Time2 (r) 0.106 0.003 30.854 0.000 0.106 0.177
#> .Time3 (r) 0.106 0.003 30.854 0.000 0.106 0.175
#> .Time4 (r) 0.106 0.003 30.854 0.000 0.106 0.164
#> i 0.519 0.027 19.007 0.000 1.000 1.000
#> s 0.016 0.002 8.790 0.000 1.000 1.000
#>
#> R-Square:
#> Estimate
#> Time1 0.830
#> Time2 0.823
#> Time3 0.825
#> Time4 0.836Comparison Table Fit Indices
- This model is much better than model 3
- Implies that having a single slope is better than just random slopes
fit.table[4, ] <- c("Full Slope", round(fitmeasures(crime.fit4, c("chisq", "df", "rmsea", "srmr", "cfi")),3))
kable(fit.table)| Model | X2 | df | RMSEA | SRMR | CFI |
|---|---|---|---|---|---|
| Intercept Only | 3461.981 | 12 | 0.55 | 0.523 | 0 |
| Random Intercept | 555.313 | 11 | 0.228 | 0.092 | 0.838 |
| Random Slope | 339.586 | 10 | 0.186 | 0.149 | 0.902 |
| Full Slope | 24.001 | 8 | 0.046 | 0.02 | 0.995 |
| NA | NA | NA | NA | NA | NA |
Comparison Table Parameters
#save the parameter estimates
crime.fit4.par <- parameterestimates(crime.fit4)
#put data in table
par.table[4, ] <- c("Full Slope",
round(crime.fit4.par$est[crime.fit4.par$lhs == "i" & crime.fit4.par$op == "~1"], 3),
round(crime.fit4.par$est[crime.fit4.par$lhs == "i" & crime.fit4.par$op == "~~" & crime.fit4.par$rhs == "i"], 3),
round(crime.fit4.par$est[crime.fit4.par$lhs == "Time1" & crime.fit4.par$op == "~~"], 3),
round(crime.fit4.par$est[crime.fit4.par$lhs == "s" & crime.fit4.par$op == "~1"], 3),
round(crime.fit4.par$est[crime.fit4.par$lhs == "s" & crime.fit4.par$op == "~~"], 3),
round(crime.fit4.par$est[crime.fit4.par$lhs == "i" & crime.fit4.par$op == "~~" & crime.fit4.par$rhs == "s"], 3))
kable(par.table)| Model | Intercept Mean | Intercept Variance | Residual Variance | Slope Mean | Slope Variance | Covariance |
|---|---|---|---|---|---|---|
| Intercept Only | 5.352 | X | 0.636 | X | X | X |
| Random Intercept | 5.352 | 0.481 | 0.155 | X | X | X |
| Random Slope | 5.262 | 0.484 | 0.11 | X | 0.025 | X |
| Full Slope | 5.183 | 0.519 | 0.106 | 0.113 | 0.016 | -0.021 |
| NA | NA | NA | NA | NA | NA | NA |
Totally Unconstrained Model
- Now the residuals are free to vary
- You want the residuals to be small and roughly equal, so this model shouldn’t be any different than the previous model
crime.model5 <- '
# intercept
i =~ 1*Time1 + 1*Time2 + 1*Time3 + 1*Time4
# slope
s =~ 0*Time1 + 1*Time2 + 2*Time3 + 3*Time4
'Totally Unconstrained Model
crime.fit5 <- growth(crime.model5,
sample.cov=crime.cov,
sample.mean=crime.mean,
sample.nobs=952)
summary(crime.fit5,
standardized = TRUE,
fit.measures = TRUE,
rsquare = TRUE)
#> lavaan 0.6-19 ended normally after 48 iterations
#>
#> Estimator ML
#> Optimization method NLMINB
#> Number of model parameters 9
#>
#> Number of observations 952
#>
#> Model Test User Model:
#>
#> Test statistic 9.137
#> Degrees of freedom 5
#> P-value (Chi-square) 0.104
#>
#> Model Test Baseline Model:
#>
#> Test statistic 3358.206
#> Degrees of freedom 6
#> P-value 0.000
#>
#> User Model versus Baseline Model:
#>
#> Comparative Fit Index (CFI) 0.999
#> Tucker-Lewis Index (TLI) 0.999
#>
#> Loglikelihood and Information Criteria:
#>
#> Loglikelihood user model (H0) -2813.783
#> Loglikelihood unrestricted model (H1) -2809.215
#>
#> Akaike (AIC) 5645.567
#> Bayesian (BIC) 5689.294
#> Sample-size adjusted Bayesian (SABIC) 5660.710
#>
#> Root Mean Square Error of Approximation:
#>
#> RMSEA 0.029
#> 90 Percent confidence interval - lower 0.000
#> 90 Percent confidence interval - upper 0.059
#> P-value H_0: RMSEA <= 0.050 0.854
#> P-value H_0: RMSEA >= 0.080 0.001
#>
#> Standardized Root Mean Square Residual:
#>
#> SRMR 0.014
#>
#> Parameter Estimates:
#>
#> Standard errors Standard
#> Information Expected
#> Information saturated (h1) model Structured
#>
#> Latent Variables:
#> Estimate Std.Err z-value P(>|z|) Std.lv Std.all
#> i =~
#> Time1 1.000 0.721 0.914
#> Time2 1.000 0.721 0.922
#> Time3 1.000 0.721 0.943
#> Time4 1.000 0.721 0.887
#> s =~
#> Time1 0.000 0.000 0.000
#> Time2 1.000 0.121 0.155
#> Time3 2.000 0.242 0.316
#> Time4 3.000 0.363 0.446
#>
#> Covariances:
#> Estimate Std.Err z-value P(>|z|) Std.lv Std.all
#> i ~~
#> s -0.020 0.006 -3.517 0.000 -0.231 -0.231
#>
#> Intercepts:
#> Estimate Std.Err z-value P(>|z|) Std.lv Std.all
#> i 5.182 0.025 207.459 0.000 7.190 7.190
#> s 0.113 0.006 18.106 0.000 0.937 0.937
#>
#> Variances:
#> Estimate Std.Err z-value P(>|z|) Std.lv Std.all
#> .Time1 0.102 0.010 10.029 0.000 0.102 0.165
#> .Time2 0.117 0.007 16.319 0.000 0.117 0.191
#> .Time3 0.087 0.006 14.268 0.000 0.087 0.149
#> .Time4 0.131 0.011 12.138 0.000 0.131 0.198
#> i 0.519 0.028 18.712 0.000 1.000 1.000
#> s 0.015 0.002 6.558 0.000 1.000 1.000
#>
#> R-Square:
#> Estimate
#> Time1 0.835
#> Time2 0.809
#> Time3 0.851
#> Time4 0.802Comparison Table Fit Indices
- This model is equal to model 4
- This result implies that your residual variances are all approximately equal
fit.table[5, ] <- c("Unconstrained", round(fitmeasures(crime.fit5, c("chisq", "df", "rmsea", "srmr", "cfi")),3))
kable(fit.table)| Model | X2 | df | RMSEA | SRMR | CFI |
|---|---|---|---|---|---|
| Intercept Only | 3461.981 | 12 | 0.55 | 0.523 | 0 |
| Random Intercept | 555.313 | 11 | 0.228 | 0.092 | 0.838 |
| Random Slope | 339.586 | 10 | 0.186 | 0.149 | 0.902 |
| Full Slope | 24.001 | 8 | 0.046 | 0.02 | 0.995 |
| Unconstrained | 9.137 | 5 | 0.029 | 0.014 | 0.999 |
Comparison Table Parameters
#save the parameter estimates
crime.fit5.par <- parameterestimates(crime.fit5)
residual_numbers <- paste(round(crime.fit5.par$est[crime.fit5.par$lhs == "Time1" & crime.fit5.par$op == "~~"], 3),
round(crime.fit5.par$est[crime.fit5.par$lhs == "Time2" & crime.fit5.par$op == "~~"], 3),
round(crime.fit5.par$est[crime.fit5.par$lhs == "Time3" & crime.fit5.par$op == "~~"], 3),
round(crime.fit5.par$est[crime.fit5.par$lhs == "Time4" & crime.fit5.par$op == "~~"], 3))
#put data in table
par.table[5, ] <- c("Unconstrained",
round(crime.fit5.par$est[crime.fit5.par$lhs == "i" & crime.fit5.par$op == "~1"], 3),
round(crime.fit5.par$est[crime.fit5.par$lhs == "i" & crime.fit5.par$op == "~~" & crime.fit5.par$rhs == "i"], 3),
residual_numbers,
round(crime.fit5.par$est[crime.fit5.par$lhs == "s" & crime.fit5.par$op == "~1"], 3),
round(crime.fit5.par$est[crime.fit5.par$lhs == "s" & crime.fit5.par$op == "~~"], 3),
round(crime.fit5.par$est[crime.fit5.par$lhs == "i" & crime.fit5.par$op == "~~" & crime.fit5.par$rhs == "s"], 3))
kable(par.table)| Model | Intercept Mean | Intercept Variance | Residual Variance | Slope Mean | Slope Variance | Covariance |
|---|---|---|---|---|---|---|
| Intercept Only | 5.352 | X | 0.636 | X | X | X |
| Random Intercept | 5.352 | 0.481 | 0.155 | X | X | X |
| Random Slope | 5.262 | 0.484 | 0.11 | X | 0.025 | X |
| Full Slope | 5.183 | 0.519 | 0.106 | 0.113 | 0.016 | -0.021 |
| Unconstrained | 5.182 | 0.519 | 0.102 0.117 0.087 0.131 | 0.113 | 0.015 | -0.02 |