Multi-Group Confirmatory Factor Analysis
lecture_mgcfa.RmdMultigroup Models
- Let’s start with some terminology specific to multigroup models: invariance = equivalence
- Under different conditions, do the measurements yield the same measurement of attributes?
- Generally, we’ve seen that latent variable models are estimating the data based on the covariances. For these models, we will also add the mean structure.
- While you can test many groups in these models, you will want to generally compare two at a time.
Mean Structure
- Mean structure represents the intercept of our manifest variables
- In regression, remember that the Y-intercept is the mean of Y (given
X = 0 or no X variables)
- That’s your best guess for what someone is going to score on that item without any other X information
- Same idea in a latent variable model - it’s the starting value for that manifest variable.
Latent Means
- Latent means are the estimated score on the latent variable for participants.
- It’s a weighted score of each item’s original value with their path coefficient, and all items are averaged together.
- We can use
lavPredict()to calculate these for us.
Multigroup Questions
- Do items act the same across groups?
- Is the factor structure the same across groups?
- Are the paths equal across groups?
- Are the latent means equal across groups?
How to MG
- First, test the model as a regular CFA with everyone in the dataset
- This model will tell you if you have problems with your CFA
- This model is the least restrictive
- Do not use grouping variables
How to MG
- Second, test each group separately with the same CFA structure to determine that each individual group fits ok.
- Fit indices often decrease slightly here, because sample size is smaller (which usually has a bit more error variance).
- Mainly, you are looking for models that completely break down
- You could have a poor fitting CFA overall and use this step to see if that’s because one group just does not fit.
How to MG
- The next steps will be to nest the two models together.
- Nesting is like stacking the models together (like pancakes).
- For the nested model steps, most people use Brown’s terminology and procedure.
How to MG
- All the possible paths:
- The whole model (the picture)
- Loadings (regression weights)
- Intercepts (y-intercept for each item)
- Error variances (variance)
- Factor variances (variances for the latents)
- Factor covariances (correlation)
- Factor means (latent means)
Equal Form / Configural Invariance
- In this model, you put the two groups together into the same model.
- You do not force any of the paths to be the same, but you are forcing the model picture to be the same.
- You are testing if both groups show the same factor structure (configuration).
Metric Invariance
- In this model, you are forcing all the factor loadings (regression weights) to be exactly the same.
- This step will tell you if the groups have the same weights for each question – or if some questions have different signs or strengths.
Scalar Invariance
- In this model, you are forcing the intercepts of the items to be the same.
- This step will tell you if items have the same starting point – remember that the y-intercept is the mean of the item.
- If a MG model is going to indicate non-invariance – this step is often the one that breaks.
Strict Factorial Invariance
- In this model, you are forcing the error variances for each item to be the same.
- This step will tell you if the variance (the spread) of the item is
the same for each group.
- If you get differences, that indicates one group has a larger range of answers than another, which indicates they are more heterogeneous.
Other Steps
- Most of the previous steps are on the manifest/measured variables only.
- Generally, we focus on those because they indicate performance of the scale.
- Population Heterogeneity:
- Equal factor variances: Testing if latents have the same set of variance – means that the overall score has the same spread
- Equal factor covariances: Testing if the correlations between factors is the same for each group
- Equal latent means: Testing if the overall latent means are equal for each group
How to Judge
- How can I tell if steps are invariant?
- You will expect fit to get worse as you go because you are being more and more restrictive.
- While we can use change in , most suggest a change in CFI > .01 to be a difference in fit.
Model Breakdown
- What do I do if steps are NOT invariant?
- Partial invariance – when strict invariance cannot be met, you can test for partial invariance
- Partial invariance occurs when most of the items are invariant but a couple.
- You have to meet the invariance criteria, so you trying to bring your bad model “up” to the invariant level
- You want to do as few of items as possible
Partial Invariance
- So, how do I test partial invariance?
- We can use modification indices to see which paths are the most problematic.
- You will change ONE item at a time.
- Slowly add items to bring CFI up to an acceptable change level (i.e. .01 or less change from the previous model).
Test Latent Means
- After saying the measured variables are partially to fully
invariant, sometimes people also calculate latent means and use
t-tests to determine if they are different by groups.
- Instead of doing all the population heterogeneity steps.
- At the minimum, it is useful to know how to calculate a weighted score for each participant.
- We normally use EFA/CFA to show that each question has a nice loading and the questions load together
- And then we use subtotals or averages to create an overall score for
each latent
- This procedure totally ignores the fact that loadings are often different.
- Why lose that information?
Let’s get started!
- Equality constraints
- We’ve talked before about setting paths equal to each other by
calling them the same parameter name
cheese =~ a\*feta + a\*swiss- So feta and swiss will be estimated at the same value.
- The entire purpose of a multigroup model is to build equality constraints
- A few packages used to do this … but have become more trouble than
they are worth, so let’s look at how to do these steps with just
lavaan.
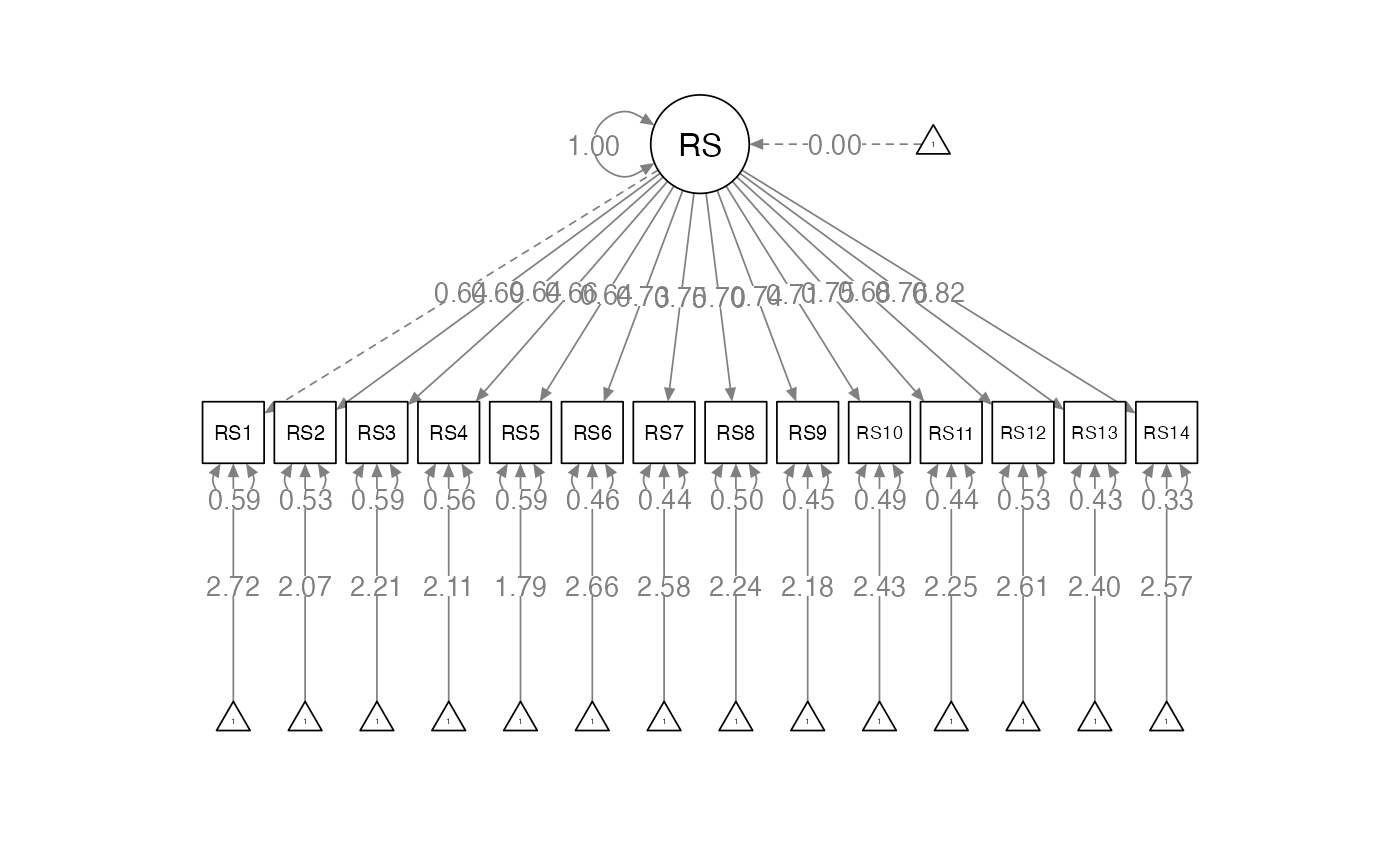
An Example
- Using the RS-14 scale: a one-factor measure of resiliency
library(lavaan)
library(rio)
res.data <- import("data/assignment_mgcfa.csv")
head(res.data)
#> Sex Ethnicity RS1 RS2 RS3 RS4 RS5 RS6 RS7 RS8 RS9 RS10 RS11 RS12 RS13 RS14
#> 1 2 0 4 4 4 4 4 4 4 4 4 4 4 4 4 4
#> 2 1 0 5 2 6 4 4 5 4 5 5 4 4 6 4 4
#> 3 2 0 7 7 7 7 2 7 7 4 3 7 7 5 7 5
#> 4 2 0 7 6 6 7 7 7 7 7 7 7 7 6 7 7
#> 5 1 0 2 2 2 2 2 2 2 2 2 2 2 2 2 2
#> 6 2 0 4 5 5 7 5 7 5 7 5 4 5 6 6 5Start with Overall CFA
- NEW:
meanstructure = TRUE - Gives you the intercepts and means in the model.
- You want to turn that one at the beginning, and you are first examining models with means, so you can tell if you have bad parameters at the start.
Start with Overall CFA
overall.model <- '
RS =~ RS1 + RS2 + RS3 + RS4 + RS5 + RS6 + RS7 + RS8 + RS9 + RS10 + RS11 + RS12 + RS13 + RS14
'
overall.fit <- cfa(model = overall.model,
data = res.data,
meanstructure = TRUE) ##this is important Examine Overall Fit
summary(overall.fit,
standardized = TRUE,
rsquare = TRUE,
fit.measure = TRUE)
#> lavaan 0.6-19 ended normally after 26 iterations
#>
#> Estimator ML
#> Optimization method NLMINB
#> Number of model parameters 42
#>
#> Number of observations 510
#>
#> Model Test User Model:
#>
#> Test statistic 368.984
#> Degrees of freedom 77
#> P-value (Chi-square) 0.000
#>
#> Model Test Baseline Model:
#>
#> Test statistic 4064.761
#> Degrees of freedom 91
#> P-value 0.000
#>
#> User Model versus Baseline Model:
#>
#> Comparative Fit Index (CFI) 0.927
#> Tucker-Lewis Index (TLI) 0.913
#>
#> Loglikelihood and Information Criteria:
#>
#> Loglikelihood user model (H0) -13050.226
#> Loglikelihood unrestricted model (H1) -12865.734
#>
#> Akaike (AIC) 26184.452
#> Bayesian (BIC) 26362.297
#> Sample-size adjusted Bayesian (SABIC) 26228.983
#>
#> Root Mean Square Error of Approximation:
#>
#> RMSEA 0.086
#> 90 Percent confidence interval - lower 0.078
#> 90 Percent confidence interval - upper 0.095
#> P-value H_0: RMSEA <= 0.050 0.000
#> P-value H_0: RMSEA >= 0.080 0.882
#>
#> Standardized Root Mean Square Residual:
#>
#> SRMR 0.041
#>
#> Parameter Estimates:
#>
#> Standard errors Standard
#> Information Expected
#> Information saturated (h1) model Structured
#>
#> Latent Variables:
#> Estimate Std.Err z-value P(>|z|) Std.lv Std.all
#> RS =~
#> RS1 1.000 1.135 0.637
#> RS2 1.230 0.091 13.529 0.000 1.397 0.685
#> RS3 1.065 0.083 12.806 0.000 1.209 0.641
#> RS4 1.231 0.094 13.150 0.000 1.398 0.662
#> RS5 1.203 0.094 12.846 0.000 1.366 0.644
#> RS6 1.218 0.085 14.258 0.000 1.383 0.732
#> RS7 1.264 0.087 14.554 0.000 1.435 0.751
#> RS8 1.207 0.087 13.836 0.000 1.371 0.705
#> RS9 1.271 0.088 14.461 0.000 1.444 0.745
#> RS10 1.193 0.086 13.946 0.000 1.355 0.712
#> RS11 1.318 0.091 14.526 0.000 1.496 0.749
#> RS12 1.156 0.086 13.494 0.000 1.312 0.683
#> RS13 1.357 0.093 14.634 0.000 1.541 0.756
#> RS14 1.335 0.086 15.587 0.000 1.515 0.821
#>
#> Intercepts:
#> Estimate Std.Err z-value P(>|z|) Std.lv Std.all
#> .RS1 4.849 0.079 61.416 0.000 4.849 2.720
#> .RS2 4.218 0.090 46.752 0.000 4.218 2.070
#> .RS3 4.163 0.084 49.853 0.000 4.163 2.208
#> .RS4 4.451 0.094 47.600 0.000 4.451 2.108
#> .RS5 3.808 0.094 40.536 0.000 3.808 1.795
#> .RS6 5.037 0.084 60.180 0.000 5.037 2.665
#> .RS7 4.937 0.085 58.353 0.000 4.937 2.584
#> .RS8 4.351 0.086 50.508 0.000 4.351 2.237
#> .RS9 4.233 0.086 49.333 0.000 4.233 2.185
#> .RS10 4.622 0.084 54.829 0.000 4.622 2.428
#> .RS11 4.486 0.088 50.739 0.000 4.486 2.247
#> .RS12 5.006 0.085 58.865 0.000 5.006 2.607
#> .RS13 4.894 0.090 54.257 0.000 4.894 2.403
#> .RS14 4.749 0.082 58.132 0.000 4.749 2.574
#>
#> Variances:
#> Estimate Std.Err z-value P(>|z|) Std.lv Std.all
#> .RS1 1.890 0.124 15.242 0.000 1.890 0.594
#> .RS2 2.200 0.146 15.025 0.000 2.200 0.530
#> .RS3 2.094 0.138 15.225 0.000 2.094 0.589
#> .RS4 2.504 0.165 15.137 0.000 2.504 0.562
#> .RS5 2.636 0.173 15.215 0.000 2.636 0.586
#> .RS6 1.660 0.113 14.740 0.000 1.660 0.465
#> .RS7 1.591 0.109 14.588 0.000 1.591 0.436
#> .RS8 1.905 0.128 14.917 0.000 1.905 0.503
#> .RS9 1.671 0.114 14.639 0.000 1.671 0.445
#> .RS10 1.788 0.120 14.875 0.000 1.788 0.493
#> .RS11 1.749 0.120 14.604 0.000 1.749 0.439
#> .RS12 1.966 0.131 15.036 0.000 1.966 0.533
#> .RS13 1.776 0.122 14.543 0.000 1.776 0.428
#> .RS14 1.107 0.081 13.753 0.000 1.107 0.325
#> RS 1.289 0.164 7.847 0.000 1.000 1.000
#>
#> R-Square:
#> Estimate
#> RS1 0.406
#> RS2 0.470
#> RS3 0.411
#> RS4 0.438
#> RS5 0.414
#> RS6 0.535
#> RS7 0.564
#> RS8 0.497
#> RS9 0.555
#> RS10 0.507
#> RS11 0.561
#> RS12 0.467
#> RS13 0.572
#> RS14 0.675Make a table of fit indices
library(knitr)
table_fit <- matrix(NA, nrow = 9, ncol = 6)
colnames(table_fit) = c("Model", "X2", "df", "CFI", "RMSEA", "SRMR")
table_fit[1, ] <- c("Overall Model", round(fitmeasures(overall.fit,
c("chisq", "df", "cfi",
"rmsea", "srmr")),3))
kable(table_fit)| Model | X2 | df | CFI | RMSEA | SRMR |
|---|---|---|---|---|---|
| Overall Model | 368.984 | 77 | 0.927 | 0.086 | 0.041 |
| NA | NA | NA | NA | NA | NA |
| NA | NA | NA | NA | NA | NA |
| NA | NA | NA | NA | NA | NA |
| NA | NA | NA | NA | NA | NA |
| NA | NA | NA | NA | NA | NA |
| NA | NA | NA | NA | NA | NA |
| NA | NA | NA | NA | NA | NA |
| NA | NA | NA | NA | NA | NA |
Men Overall Summary
men.fit <- cfa(model = overall.model,
data = res.data[res.data$Sex == "Men" , ],
meanstructure = TRUE)
summary(men.fit,
standardized = TRUE,
rsquare = TRUE,
fit.measure = TRUE)
#> lavaan 0.6-19 ended normally after 25 iterations
#>
#> Estimator ML
#> Optimization method NLMINB
#> Number of model parameters 42
#>
#> Number of observations 244
#>
#> Model Test User Model:
#>
#> Test statistic 271.457
#> Degrees of freedom 77
#> P-value (Chi-square) 0.000
#>
#> Model Test Baseline Model:
#>
#> Test statistic 2515.572
#> Degrees of freedom 91
#> P-value 0.000
#>
#> User Model versus Baseline Model:
#>
#> Comparative Fit Index (CFI) 0.920
#> Tucker-Lewis Index (TLI) 0.905
#>
#> Loglikelihood and Information Criteria:
#>
#> Loglikelihood user model (H0) -6043.672
#> Loglikelihood unrestricted model (H1) -5907.944
#>
#> Akaike (AIC) 12171.345
#> Bayesian (BIC) 12318.226
#> Sample-size adjusted Bayesian (SABIC) 12185.091
#>
#> Root Mean Square Error of Approximation:
#>
#> RMSEA 0.102
#> 90 Percent confidence interval - lower 0.089
#> 90 Percent confidence interval - upper 0.115
#> P-value H_0: RMSEA <= 0.050 0.000
#> P-value H_0: RMSEA >= 0.080 0.997
#>
#> Standardized Root Mean Square Residual:
#>
#> SRMR 0.041
#>
#> Parameter Estimates:
#>
#> Standard errors Standard
#> Information Expected
#> Information saturated (h1) model Structured
#>
#> Latent Variables:
#> Estimate Std.Err z-value P(>|z|) Std.lv Std.all
#> RS =~
#> RS1 1.000 1.293 0.701
#> RS2 1.190 0.105 11.360 0.000 1.538 0.755
#> RS3 1.015 0.097 10.467 0.000 1.313 0.694
#> RS4 1.131 0.108 10.498 0.000 1.462 0.696
#> RS5 1.098 0.108 10.168 0.000 1.420 0.674
#> RS6 1.122 0.101 11.093 0.000 1.451 0.737
#> RS7 1.125 0.100 11.204 0.000 1.455 0.745
#> RS8 1.188 0.101 11.799 0.000 1.536 0.785
#> RS9 1.200 0.098 12.228 0.000 1.552 0.815
#> RS10 1.103 0.097 11.354 0.000 1.426 0.755
#> RS11 1.185 0.101 11.757 0.000 1.533 0.782
#> RS12 1.213 0.102 11.877 0.000 1.568 0.791
#> RS13 1.331 0.107 12.497 0.000 1.722 0.833
#> RS14 1.267 0.101 12.546 0.000 1.639 0.837
#>
#> Intercepts:
#> Estimate Std.Err z-value P(>|z|) Std.lv Std.all
#> .RS1 4.697 0.118 39.741 0.000 4.697 2.544
#> .RS2 4.197 0.130 32.180 0.000 4.197 2.060
#> .RS3 4.242 0.121 35.035 0.000 4.242 2.243
#> .RS4 4.615 0.134 34.330 0.000 4.615 2.198
#> .RS5 3.971 0.135 29.448 0.000 3.971 1.885
#> .RS6 4.889 0.126 38.788 0.000 4.889 2.483
#> .RS7 4.820 0.125 38.520 0.000 4.820 2.466
#> .RS8 4.422 0.125 35.315 0.000 4.422 2.261
#> .RS9 4.299 0.122 35.259 0.000 4.299 2.257
#> .RS10 4.537 0.121 37.516 0.000 4.537 2.402
#> .RS11 4.467 0.125 35.614 0.000 4.467 2.280
#> .RS12 4.820 0.127 37.954 0.000 4.820 2.430
#> .RS13 4.799 0.132 36.291 0.000 4.799 2.323
#> .RS14 4.697 0.125 37.467 0.000 4.697 2.399
#>
#> Variances:
#> Estimate Std.Err z-value P(>|z|) Std.lv Std.all
#> .RS1 1.736 0.165 10.517 0.000 1.736 0.509
#> .RS2 1.783 0.173 10.317 0.000 1.783 0.430
#> .RS3 1.852 0.176 10.535 0.000 1.852 0.518
#> .RS4 2.270 0.216 10.529 0.000 2.270 0.515
#> .RS5 2.421 0.229 10.589 0.000 2.421 0.546
#> .RS6 1.771 0.170 10.393 0.000 1.771 0.457
#> .RS7 1.702 0.164 10.363 0.000 1.702 0.446
#> .RS8 1.466 0.144 10.162 0.000 1.466 0.383
#> .RS9 1.219 0.122 9.960 0.000 1.219 0.336
#> .RS10 1.535 0.149 10.319 0.000 1.535 0.430
#> .RS11 1.489 0.146 10.179 0.000 1.489 0.388
#> .RS12 1.475 0.146 10.130 0.000 1.475 0.375
#> .RS13 1.303 0.133 9.795 0.000 1.303 0.305
#> .RS14 1.149 0.118 9.762 0.000 1.149 0.300
#> RS 1.672 0.270 6.188 0.000 1.000 1.000
#>
#> R-Square:
#> Estimate
#> RS1 0.491
#> RS2 0.570
#> RS3 0.482
#> RS4 0.485
#> RS5 0.454
#> RS6 0.543
#> RS7 0.554
#> RS8 0.617
#> RS9 0.664
#> RS10 0.570
#> RS11 0.612
#> RS12 0.625
#> RS13 0.695
#> RS14 0.700Women Overall Summary
women.fit <- cfa(model = overall.model,
data = res.data[res.data$Sex == "Women" , ],
meanstructure = TRUE)
summary(women.fit,
standardized = TRUE,
rsquare = TRUE,
fit.measure = TRUE)
#> lavaan 0.6-19 ended normally after 29 iterations
#>
#> Estimator ML
#> Optimization method NLMINB
#> Number of model parameters 42
#>
#> Number of observations 266
#>
#> Model Test User Model:
#>
#> Test statistic 258.610
#> Degrees of freedom 77
#> P-value (Chi-square) 0.000
#>
#> Model Test Baseline Model:
#>
#> Test statistic 1813.360
#> Degrees of freedom 91
#> P-value 0.000
#>
#> User Model versus Baseline Model:
#>
#> Comparative Fit Index (CFI) 0.895
#> Tucker-Lewis Index (TLI) 0.875
#>
#> Loglikelihood and Information Criteria:
#>
#> Loglikelihood user model (H0) -6938.738
#> Loglikelihood unrestricted model (H1) -6809.434
#>
#> Akaike (AIC) 13961.477
#> Bayesian (BIC) 14111.984
#> Sample-size adjusted Bayesian (SABIC) 13978.820
#>
#> Root Mean Square Error of Approximation:
#>
#> RMSEA 0.094
#> 90 Percent confidence interval - lower 0.082
#> 90 Percent confidence interval - upper 0.107
#> P-value H_0: RMSEA <= 0.050 0.000
#> P-value H_0: RMSEA >= 0.080 0.968
#>
#> Standardized Root Mean Square Residual:
#>
#> SRMR 0.052
#>
#> Parameter Estimates:
#>
#> Standard errors Standard
#> Information Expected
#> Information saturated (h1) model Structured
#>
#> Latent Variables:
#> Estimate Std.Err z-value P(>|z|) Std.lv Std.all
#> RS =~
#> RS1 1.000 0.958 0.560
#> RS2 1.291 0.163 7.908 0.000 1.237 0.607
#> RS3 1.140 0.149 7.675 0.000 1.093 0.582
#> RS4 1.401 0.172 8.157 0.000 1.342 0.636
#> RS5 1.381 0.172 8.046 0.000 1.323 0.623
#> RS6 1.381 0.155 8.933 0.000 1.323 0.733
#> RS7 1.485 0.162 9.150 0.000 1.423 0.764
#> RS8 1.259 0.156 8.055 0.000 1.206 0.624
#> RS9 1.400 0.164 8.543 0.000 1.341 0.682
#> RS10 1.333 0.158 8.426 0.000 1.278 0.668
#> RS11 1.503 0.172 8.754 0.000 1.440 0.709
#> RS12 1.106 0.145 7.609 0.000 1.060 0.575
#> RS13 1.421 0.167 8.513 0.000 1.362 0.679
#> RS14 1.470 0.155 9.476 0.000 1.408 0.813
#>
#> Intercepts:
#> Estimate Std.Err z-value P(>|z|) Std.lv Std.all
#> .RS1 4.989 0.105 47.546 0.000 4.989 2.915
#> .RS2 4.237 0.125 33.918 0.000 4.237 2.080
#> .RS3 4.090 0.115 35.528 0.000 4.090 2.178
#> .RS4 4.301 0.129 33.220 0.000 4.301 2.037
#> .RS5 3.658 0.130 28.090 0.000 3.658 1.722
#> .RS6 5.173 0.111 46.757 0.000 5.173 2.867
#> .RS7 5.045 0.114 44.162 0.000 5.045 2.708
#> .RS8 4.286 0.119 36.153 0.000 4.286 2.217
#> .RS9 4.173 0.121 34.619 0.000 4.173 2.123
#> .RS10 4.699 0.117 40.054 0.000 4.699 2.456
#> .RS11 4.504 0.124 36.179 0.000 4.504 2.218
#> .RS12 5.177 0.113 45.781 0.000 5.177 2.807
#> .RS13 4.981 0.123 40.489 0.000 4.981 2.483
#> .RS14 4.797 0.106 45.141 0.000 4.797 2.768
#>
#> Variances:
#> Estimate Std.Err z-value P(>|z|) Std.lv Std.all
#> .RS1 2.010 0.181 11.094 0.000 2.010 0.686
#> .RS2 2.620 0.239 10.972 0.000 2.620 0.631
#> .RS3 2.332 0.211 11.041 0.000 2.332 0.661
#> .RS4 2.657 0.244 10.881 0.000 2.657 0.596
#> .RS5 2.760 0.253 10.924 0.000 2.760 0.612
#> .RS6 1.505 0.145 10.414 0.000 1.505 0.462
#> .RS7 1.447 0.142 10.186 0.000 1.447 0.417
#> .RS8 2.283 0.209 10.921 0.000 2.283 0.611
#> .RS9 2.066 0.193 10.696 0.000 2.066 0.534
#> .RS10 2.028 0.189 10.759 0.000 2.028 0.554
#> .RS11 2.048 0.194 10.559 0.000 2.048 0.497
#> .RS12 2.277 0.206 11.059 0.000 2.277 0.669
#> .RS13 2.172 0.203 10.712 0.000 2.172 0.540
#> .RS14 1.020 0.106 9.659 0.000 1.020 0.340
#> RS 0.918 0.191 4.804 0.000 1.000 1.000
#>
#> R-Square:
#> Estimate
#> RS1 0.314
#> RS2 0.369
#> RS3 0.339
#> RS4 0.404
#> RS5 0.388
#> RS6 0.538
#> RS7 0.583
#> RS8 0.389
#> RS9 0.466
#> RS10 0.446
#> RS11 0.503
#> RS12 0.331
#> RS13 0.460
#> RS14 0.660Add the fit to table
table_fit[2, ] <- c("Men Model", round(fitmeasures(men.fit,
c("chisq", "df", "cfi",
"rmsea", "srmr")),3))
table_fit[3, ] <- c("Women Model", round(fitmeasures(women.fit,
c("chisq", "df", "cfi",
"rmsea", "srmr")),3))
kable(table_fit)| Model | X2 | df | CFI | RMSEA | SRMR |
|---|---|---|---|---|---|
| Overall Model | 368.984 | 77 | 0.927 | 0.086 | 0.041 |
| Men Model | 271.457 | 77 | 0.92 | 0.102 | 0.041 |
| Women Model | 258.61 | 77 | 0.895 | 0.094 | 0.052 |
| NA | NA | NA | NA | NA | NA |
| NA | NA | NA | NA | NA | NA |
| NA | NA | NA | NA | NA | NA |
| NA | NA | NA | NA | NA | NA |
| NA | NA | NA | NA | NA | NA |
| NA | NA | NA | NA | NA | NA |
Configural Invariance
- Both groups “pancaked” together
configural.fit <- cfa(model = overall.model,
data = res.data,
meanstructure = TRUE,
group = "Sex")
summary(configural.fit,
standardized = TRUE,
rsquare = TRUE,
fit.measure = TRUE)
#> lavaan 0.6-19 ended normally after 49 iterations
#>
#> Estimator ML
#> Optimization method NLMINB
#> Number of model parameters 84
#>
#> Number of observations per group:
#> Women 266
#> Men 244
#>
#> Model Test User Model:
#>
#> Test statistic 530.067
#> Degrees of freedom 154
#> P-value (Chi-square) 0.000
#> Test statistic for each group:
#> Women 258.610
#> Men 271.457
#>
#> Model Test Baseline Model:
#>
#> Test statistic 4328.931
#> Degrees of freedom 182
#> P-value 0.000
#>
#> User Model versus Baseline Model:
#>
#> Comparative Fit Index (CFI) 0.909
#> Tucker-Lewis Index (TLI) 0.893
#>
#> Loglikelihood and Information Criteria:
#>
#> Loglikelihood user model (H0) -12982.411
#> Loglikelihood unrestricted model (H1) -12717.377
#>
#> Akaike (AIC) 26132.822
#> Bayesian (BIC) 26488.512
#> Sample-size adjusted Bayesian (SABIC) 26221.885
#>
#> Root Mean Square Error of Approximation:
#>
#> RMSEA 0.098
#> 90 Percent confidence interval - lower 0.089
#> 90 Percent confidence interval - upper 0.107
#> P-value H_0: RMSEA <= 0.050 0.000
#> P-value H_0: RMSEA >= 0.080 0.999
#>
#> Standardized Root Mean Square Residual:
#>
#> SRMR 0.047
#>
#> Parameter Estimates:
#>
#> Standard errors Standard
#> Information Expected
#> Information saturated (h1) model Structured
#>
#>
#> Group 1 [Women]:
#>
#> Latent Variables:
#> Estimate Std.Err z-value P(>|z|) Std.lv Std.all
#> RS =~
#> RS1 1.000 0.958 0.560
#> RS2 1.291 0.163 7.908 0.000 1.237 0.607
#> RS3 1.140 0.149 7.675 0.000 1.093 0.582
#> RS4 1.401 0.172 8.157 0.000 1.342 0.636
#> RS5 1.381 0.172 8.046 0.000 1.323 0.623
#> RS6 1.381 0.155 8.933 0.000 1.323 0.733
#> RS7 1.485 0.162 9.150 0.000 1.423 0.764
#> RS8 1.259 0.156 8.055 0.000 1.206 0.624
#> RS9 1.400 0.164 8.543 0.000 1.341 0.682
#> RS10 1.333 0.158 8.426 0.000 1.278 0.668
#> RS11 1.503 0.172 8.754 0.000 1.440 0.709
#> RS12 1.106 0.145 7.609 0.000 1.060 0.575
#> RS13 1.421 0.167 8.513 0.000 1.362 0.679
#> RS14 1.470 0.155 9.476 0.000 1.408 0.813
#>
#> Intercepts:
#> Estimate Std.Err z-value P(>|z|) Std.lv Std.all
#> .RS1 4.989 0.105 47.546 0.000 4.989 2.915
#> .RS2 4.237 0.125 33.918 0.000 4.237 2.080
#> .RS3 4.090 0.115 35.528 0.000 4.090 2.178
#> .RS4 4.301 0.129 33.220 0.000 4.301 2.037
#> .RS5 3.658 0.130 28.090 0.000 3.658 1.722
#> .RS6 5.173 0.111 46.757 0.000 5.173 2.867
#> .RS7 5.045 0.114 44.162 0.000 5.045 2.708
#> .RS8 4.286 0.119 36.153 0.000 4.286 2.217
#> .RS9 4.173 0.121 34.619 0.000 4.173 2.123
#> .RS10 4.699 0.117 40.054 0.000 4.699 2.456
#> .RS11 4.504 0.124 36.179 0.000 4.504 2.218
#> .RS12 5.177 0.113 45.781 0.000 5.177 2.807
#> .RS13 4.981 0.123 40.489 0.000 4.981 2.483
#> .RS14 4.797 0.106 45.141 0.000 4.797 2.768
#>
#> Variances:
#> Estimate Std.Err z-value P(>|z|) Std.lv Std.all
#> .RS1 2.010 0.181 11.094 0.000 2.010 0.686
#> .RS2 2.620 0.239 10.972 0.000 2.620 0.631
#> .RS3 2.332 0.211 11.041 0.000 2.332 0.661
#> .RS4 2.657 0.244 10.881 0.000 2.657 0.596
#> .RS5 2.760 0.253 10.924 0.000 2.760 0.612
#> .RS6 1.505 0.145 10.414 0.000 1.505 0.462
#> .RS7 1.447 0.142 10.186 0.000 1.447 0.417
#> .RS8 2.283 0.209 10.921 0.000 2.283 0.611
#> .RS9 2.066 0.193 10.696 0.000 2.066 0.534
#> .RS10 2.028 0.189 10.759 0.000 2.028 0.554
#> .RS11 2.048 0.194 10.559 0.000 2.048 0.497
#> .RS12 2.277 0.206 11.059 0.000 2.277 0.669
#> .RS13 2.172 0.203 10.712 0.000 2.172 0.540
#> .RS14 1.020 0.106 9.659 0.000 1.020 0.340
#> RS 0.918 0.191 4.804 0.000 1.000 1.000
#>
#> R-Square:
#> Estimate
#> RS1 0.314
#> RS2 0.369
#> RS3 0.339
#> RS4 0.404
#> RS5 0.388
#> RS6 0.538
#> RS7 0.583
#> RS8 0.389
#> RS9 0.466
#> RS10 0.446
#> RS11 0.503
#> RS12 0.331
#> RS13 0.460
#> RS14 0.660
#>
#>
#> Group 2 [Men]:
#>
#> Latent Variables:
#> Estimate Std.Err z-value P(>|z|) Std.lv Std.all
#> RS =~
#> RS1 1.000 1.293 0.701
#> RS2 1.190 0.105 11.360 0.000 1.538 0.755
#> RS3 1.015 0.097 10.467 0.000 1.313 0.694
#> RS4 1.131 0.108 10.498 0.000 1.462 0.696
#> RS5 1.098 0.108 10.168 0.000 1.420 0.674
#> RS6 1.122 0.101 11.093 0.000 1.451 0.737
#> RS7 1.125 0.100 11.204 0.000 1.455 0.745
#> RS8 1.188 0.101 11.799 0.000 1.536 0.785
#> RS9 1.200 0.098 12.228 0.000 1.552 0.815
#> RS10 1.103 0.097 11.354 0.000 1.426 0.755
#> RS11 1.185 0.101 11.757 0.000 1.533 0.782
#> RS12 1.213 0.102 11.877 0.000 1.568 0.791
#> RS13 1.331 0.107 12.497 0.000 1.722 0.833
#> RS14 1.267 0.101 12.546 0.000 1.639 0.837
#>
#> Intercepts:
#> Estimate Std.Err z-value P(>|z|) Std.lv Std.all
#> .RS1 4.697 0.118 39.741 0.000 4.697 2.544
#> .RS2 4.197 0.130 32.180 0.000 4.197 2.060
#> .RS3 4.242 0.121 35.035 0.000 4.242 2.243
#> .RS4 4.615 0.134 34.330 0.000 4.615 2.198
#> .RS5 3.971 0.135 29.448 0.000 3.971 1.885
#> .RS6 4.889 0.126 38.788 0.000 4.889 2.483
#> .RS7 4.820 0.125 38.520 0.000 4.820 2.466
#> .RS8 4.422 0.125 35.315 0.000 4.422 2.261
#> .RS9 4.299 0.122 35.259 0.000 4.299 2.257
#> .RS10 4.537 0.121 37.516 0.000 4.537 2.402
#> .RS11 4.467 0.125 35.614 0.000 4.467 2.280
#> .RS12 4.820 0.127 37.954 0.000 4.820 2.430
#> .RS13 4.799 0.132 36.291 0.000 4.799 2.323
#> .RS14 4.697 0.125 37.467 0.000 4.697 2.399
#>
#> Variances:
#> Estimate Std.Err z-value P(>|z|) Std.lv Std.all
#> .RS1 1.736 0.165 10.517 0.000 1.736 0.509
#> .RS2 1.783 0.173 10.317 0.000 1.783 0.430
#> .RS3 1.852 0.176 10.535 0.000 1.852 0.518
#> .RS4 2.270 0.216 10.529 0.000 2.270 0.515
#> .RS5 2.421 0.229 10.589 0.000 2.421 0.546
#> .RS6 1.771 0.170 10.393 0.000 1.771 0.457
#> .RS7 1.702 0.164 10.363 0.000 1.702 0.446
#> .RS8 1.466 0.144 10.162 0.000 1.466 0.383
#> .RS9 1.219 0.122 9.960 0.000 1.219 0.336
#> .RS10 1.535 0.149 10.319 0.000 1.535 0.430
#> .RS11 1.489 0.146 10.179 0.000 1.489 0.388
#> .RS12 1.475 0.146 10.130 0.000 1.475 0.375
#> .RS13 1.303 0.133 9.795 0.000 1.303 0.305
#> .RS14 1.149 0.118 9.762 0.000 1.149 0.300
#> RS 1.672 0.270 6.188 0.000 1.000 1.000
#>
#> R-Square:
#> Estimate
#> RS1 0.491
#> RS2 0.570
#> RS3 0.482
#> RS4 0.485
#> RS5 0.454
#> RS6 0.543
#> RS7 0.554
#> RS8 0.617
#> RS9 0.664
#> RS10 0.570
#> RS11 0.612
#> RS12 0.625
#> RS13 0.695
#> RS14 0.700Add the fit to table
table_fit[4, ] <- c("Configural Model", round(fitmeasures(configural.fit,
c("chisq", "df", "cfi",
"rmsea", "srmr")),3))
kable(table_fit)| Model | X2 | df | CFI | RMSEA | SRMR |
|---|---|---|---|---|---|
| Overall Model | 368.984 | 77 | 0.927 | 0.086 | 0.041 |
| Men Model | 271.457 | 77 | 0.92 | 0.102 | 0.041 |
| Women Model | 258.61 | 77 | 0.895 | 0.094 | 0.052 |
| Configural Model | 530.067 | 154 | 0.909 | 0.098 | 0.047 |
| NA | NA | NA | NA | NA | NA |
| NA | NA | NA | NA | NA | NA |
| NA | NA | NA | NA | NA | NA |
| NA | NA | NA | NA | NA | NA |
| NA | NA | NA | NA | NA | NA |
Metric Invariance
- Are the factor loadings the same?
metric.fit <- cfa(model = overall.model,
data = res.data,
meanstructure = TRUE,
group = "Sex",
group.equal = c("loadings"))
summary(metric.fit,
standardized = TRUE,
rsquare = TRUE,
fit.measure = TRUE)
#> lavaan 0.6-19 ended normally after 36 iterations
#>
#> Estimator ML
#> Optimization method NLMINB
#> Number of model parameters 84
#> Number of equality constraints 13
#>
#> Number of observations per group:
#> Women 266
#> Men 244
#>
#> Model Test User Model:
#>
#> Test statistic 545.518
#> Degrees of freedom 167
#> P-value (Chi-square) 0.000
#> Test statistic for each group:
#> Women 268.133
#> Men 277.385
#>
#> Model Test Baseline Model:
#>
#> Test statistic 4328.931
#> Degrees of freedom 182
#> P-value 0.000
#>
#> User Model versus Baseline Model:
#>
#> Comparative Fit Index (CFI) 0.909
#> Tucker-Lewis Index (TLI) 0.901
#>
#> Loglikelihood and Information Criteria:
#>
#> Loglikelihood user model (H0) -12990.137
#> Loglikelihood unrestricted model (H1) -12717.377
#>
#> Akaike (AIC) 26122.273
#> Bayesian (BIC) 26422.916
#> Sample-size adjusted Bayesian (SABIC) 26197.552
#>
#> Root Mean Square Error of Approximation:
#>
#> RMSEA 0.094
#> 90 Percent confidence interval - lower 0.086
#> 90 Percent confidence interval - upper 0.103
#> P-value H_0: RMSEA <= 0.050 0.000
#> P-value H_0: RMSEA >= 0.080 0.996
#>
#> Standardized Root Mean Square Residual:
#>
#> SRMR 0.057
#>
#> Parameter Estimates:
#>
#> Standard errors Standard
#> Information Expected
#> Information saturated (h1) model Structured
#>
#>
#> Group 1 [Women]:
#>
#> Latent Variables:
#> Estimate Std.Err z-value P(>|z|) Std.lv Std.all
#> RS =~
#> RS1 1.000 1.047 0.595
#> RS2 (.p2.) 1.232 0.089 13.828 0.000 1.290 0.624
#> RS3 (.p3.) 1.063 0.082 12.984 0.000 1.113 0.589
#> RS4 (.p4.) 1.229 0.092 13.338 0.000 1.287 0.619
#> RS5 (.p5.) 1.202 0.092 13.025 0.000 1.258 0.603
#> RS6 (.p6.) 1.221 0.085 14.407 0.000 1.279 0.720
#> RS7 (.p7.) 1.269 0.086 14.698 0.000 1.328 0.738
#> RS8 (.p8.) 1.219 0.086 14.256 0.000 1.277 0.646
#> RS9 (.p9.) 1.270 0.085 14.871 0.000 1.330 0.679
#> RS10 (.10.) 1.184 0.084 14.133 0.000 1.240 0.656
#> RS11 (.11.) 1.296 0.088 14.662 0.000 1.357 0.686
#> RS12 (.12.) 1.187 0.084 14.058 0.000 1.243 0.636
#> RS13 (.13.) 1.370 0.091 15.075 0.000 1.434 0.698
#> RS14 (.14.) 1.340 0.085 15.774 0.000 1.403 0.811
#>
#> Intercepts:
#> Estimate Std.Err z-value P(>|z|) Std.lv Std.all
#> .RS1 4.989 0.108 46.212 0.000 4.989 2.833
#> .RS2 4.237 0.127 33.447 0.000 4.237 2.051
#> .RS3 4.090 0.116 35.332 0.000 4.090 2.166
#> .RS4 4.301 0.128 33.724 0.000 4.301 2.068
#> .RS5 3.658 0.128 28.593 0.000 3.658 1.753
#> .RS6 5.173 0.109 47.491 0.000 5.173 2.912
#> .RS7 5.045 0.110 45.709 0.000 5.045 2.803
#> .RS8 4.286 0.121 35.351 0.000 4.286 2.167
#> .RS9 4.173 0.120 34.740 0.000 4.173 2.130
#> .RS10 4.699 0.116 40.534 0.000 4.699 2.485
#> .RS11 4.504 0.121 37.122 0.000 4.504 2.276
#> .RS12 5.177 0.120 43.174 0.000 5.177 2.647
#> .RS13 4.981 0.126 39.540 0.000 4.981 2.424
#> .RS14 4.797 0.106 45.258 0.000 4.797 2.775
#>
#> Variances:
#> Estimate Std.Err z-value P(>|z|) Std.lv Std.all
#> .RS1 2.004 0.182 11.028 0.000 2.004 0.646
#> .RS2 2.605 0.238 10.946 0.000 2.605 0.610
#> .RS3 2.327 0.211 11.043 0.000 2.327 0.653
#> .RS4 2.670 0.244 10.961 0.000 2.670 0.617
#> .RS5 2.771 0.252 11.006 0.000 2.771 0.636
#> .RS6 1.520 0.144 10.533 0.000 1.520 0.482
#> .RS7 1.476 0.142 10.422 0.000 1.476 0.455
#> .RS8 2.279 0.210 10.876 0.000 2.279 0.583
#> .RS9 2.070 0.193 10.749 0.000 2.070 0.539
#> .RS10 2.037 0.188 10.838 0.000 2.037 0.570
#> .RS11 2.073 0.194 10.715 0.000 2.073 0.530
#> .RS12 2.279 0.209 10.910 0.000 2.279 0.596
#> .RS13 2.165 0.203 10.660 0.000 2.165 0.513
#> .RS14 1.021 0.105 9.740 0.000 1.021 0.342
#> RS 1.096 0.156 7.018 0.000 1.000 1.000
#>
#> R-Square:
#> Estimate
#> RS1 0.354
#> RS2 0.390
#> RS3 0.347
#> RS4 0.383
#> RS5 0.364
#> RS6 0.518
#> RS7 0.545
#> RS8 0.417
#> RS9 0.461
#> RS10 0.430
#> RS11 0.470
#> RS12 0.404
#> RS13 0.487
#> RS14 0.658
#>
#>
#> Group 2 [Men]:
#>
#> Latent Variables:
#> Estimate Std.Err z-value P(>|z|) Std.lv Std.all
#> RS =~
#> RS1 1.000 1.225 0.680
#> RS2 (.p2.) 1.232 0.089 13.828 0.000 1.510 0.749
#> RS3 (.p3.) 1.063 0.082 12.984 0.000 1.302 0.692
#> RS4 (.p4.) 1.229 0.092 13.338 0.000 1.506 0.707
#> RS5 (.p5.) 1.202 0.092 13.025 0.000 1.472 0.687
#> RS6 (.p6.) 1.221 0.085 14.407 0.000 1.497 0.748
#> RS7 (.p7.) 1.269 0.086 14.698 0.000 1.555 0.767
#> RS8 (.p8.) 1.219 0.086 14.256 0.000 1.494 0.776
#> RS9 (.p9.) 1.270 0.085 14.871 0.000 1.556 0.815
#> RS10 (.10.) 1.184 0.084 14.133 0.000 1.451 0.761
#> RS11 (.11.) 1.296 0.088 14.662 0.000 1.588 0.794
#> RS12 (.12.) 1.187 0.084 14.058 0.000 1.455 0.764
#> RS13 (.13.) 1.370 0.091 15.075 0.000 1.678 0.825
#> RS14 (.14.) 1.340 0.085 15.774 0.000 1.642 0.836
#>
#> Intercepts:
#> Estimate Std.Err z-value P(>|z|) Std.lv Std.all
#> .RS1 4.697 0.115 40.725 0.000 4.697 2.607
#> .RS2 4.197 0.129 32.526 0.000 4.197 2.082
#> .RS3 4.242 0.121 35.202 0.000 4.242 2.254
#> .RS4 4.615 0.136 33.863 0.000 4.615 2.168
#> .RS5 3.971 0.137 28.963 0.000 3.971 1.854
#> .RS6 4.889 0.128 38.172 0.000 4.889 2.444
#> .RS7 4.820 0.130 37.142 0.000 4.820 2.378
#> .RS8 4.422 0.123 35.886 0.000 4.422 2.297
#> .RS9 4.299 0.122 35.175 0.000 4.299 2.252
#> .RS10 4.537 0.122 37.150 0.000 4.537 2.378
#> .RS11 4.467 0.128 34.892 0.000 4.467 2.234
#> .RS12 4.820 0.122 39.522 0.000 4.820 2.530
#> .RS13 4.799 0.130 36.857 0.000 4.799 2.360
#> .RS14 4.697 0.126 37.373 0.000 4.697 2.393
#>
#> Variances:
#> Estimate Std.Err z-value P(>|z|) Std.lv Std.all
#> .RS1 1.744 0.165 10.580 0.000 1.744 0.537
#> .RS2 1.783 0.172 10.353 0.000 1.783 0.439
#> .RS3 1.847 0.175 10.549 0.000 1.847 0.521
#> .RS4 2.263 0.215 10.504 0.000 2.263 0.499
#> .RS5 2.420 0.229 10.561 0.000 2.420 0.527
#> .RS6 1.763 0.170 10.360 0.000 1.763 0.440
#> .RS7 1.691 0.165 10.275 0.000 1.691 0.412
#> .RS8 1.472 0.144 10.222 0.000 1.472 0.397
#> .RS9 1.223 0.123 9.969 0.000 1.223 0.336
#> .RS10 1.532 0.149 10.301 0.000 1.532 0.421
#> .RS11 1.476 0.146 10.119 0.000 1.476 0.369
#> .RS12 1.512 0.147 10.286 0.000 1.512 0.417
#> .RS13 1.320 0.134 9.886 0.000 1.320 0.319
#> .RS14 1.158 0.118 9.788 0.000 1.158 0.301
#> RS 1.502 0.215 6.973 0.000 1.000 1.000
#>
#> R-Square:
#> Estimate
#> RS1 0.463
#> RS2 0.561
#> RS3 0.479
#> RS4 0.501
#> RS5 0.473
#> RS6 0.560
#> RS7 0.588
#> RS8 0.603
#> RS9 0.664
#> RS10 0.579
#> RS11 0.631
#> RS12 0.583
#> RS13 0.681
#> RS14 0.699Add the fit to table
table_fit[5, ] <- c("Metric Model", round(fitmeasures(metric.fit,
c("chisq", "df", "cfi",
"rmsea", "srmr")),3))
kable(table_fit)| Model | X2 | df | CFI | RMSEA | SRMR |
|---|---|---|---|---|---|
| Overall Model | 368.984 | 77 | 0.927 | 0.086 | 0.041 |
| Men Model | 271.457 | 77 | 0.92 | 0.102 | 0.041 |
| Women Model | 258.61 | 77 | 0.895 | 0.094 | 0.052 |
| Configural Model | 530.067 | 154 | 0.909 | 0.098 | 0.047 |
| Metric Model | 545.518 | 167 | 0.909 | 0.094 | 0.057 |
| NA | NA | NA | NA | NA | NA |
| NA | NA | NA | NA | NA | NA |
| NA | NA | NA | NA | NA | NA |
| NA | NA | NA | NA | NA | NA |
Scalar Invariance
- Are the item intercepts the same?
scalar.fit <- cfa(model = overall.model,
data = res.data,
meanstructure = TRUE,
group = "Sex",
group.equal = c("loadings", "intercepts"))
summary(scalar.fit,
standardized = TRUE,
rsquare = TRUE,
fit.measure = TRUE)
#> lavaan 0.6-19 ended normally after 47 iterations
#>
#> Estimator ML
#> Optimization method NLMINB
#> Number of model parameters 85
#> Number of equality constraints 27
#>
#> Number of observations per group:
#> Women 266
#> Men 244
#>
#> Model Test User Model:
#>
#> Test statistic 585.327
#> Degrees of freedom 180
#> P-value (Chi-square) 0.000
#> Test statistic for each group:
#> Women 289.405
#> Men 295.921
#>
#> Model Test Baseline Model:
#>
#> Test statistic 4328.931
#> Degrees of freedom 182
#> P-value 0.000
#>
#> User Model versus Baseline Model:
#>
#> Comparative Fit Index (CFI) 0.902
#> Tucker-Lewis Index (TLI) 0.901
#>
#> Loglikelihood and Information Criteria:
#>
#> Loglikelihood user model (H0) -13010.041
#> Loglikelihood unrestricted model (H1) -12717.377
#>
#> Akaike (AIC) 26136.082
#> Bayesian (BIC) 26381.678
#> Sample-size adjusted Bayesian (SABIC) 26197.577
#>
#> Root Mean Square Error of Approximation:
#>
#> RMSEA 0.094
#> 90 Percent confidence interval - lower 0.086
#> 90 Percent confidence interval - upper 0.103
#> P-value H_0: RMSEA <= 0.050 0.000
#> P-value H_0: RMSEA >= 0.080 0.997
#>
#> Standardized Root Mean Square Residual:
#>
#> SRMR 0.060
#>
#> Parameter Estimates:
#>
#> Standard errors Standard
#> Information Expected
#> Information saturated (h1) model Structured
#>
#>
#> Group 1 [Women]:
#>
#> Latent Variables:
#> Estimate Std.Err z-value P(>|z|) Std.lv Std.all
#> RS =~
#> RS1 1.000 1.049 0.594
#> RS2 (.p2.) 1.229 0.089 13.815 0.000 1.289 0.624
#> RS3 (.p3.) 1.057 0.082 12.939 0.000 1.110 0.587
#> RS4 (.p4.) 1.221 0.092 13.252 0.000 1.281 0.614
#> RS5 (.p5.) 1.193 0.092 12.939 0.000 1.252 0.598
#> RS6 (.p6.) 1.221 0.085 14.382 0.000 1.281 0.719
#> RS7 (.p7.) 1.268 0.086 14.682 0.000 1.330 0.738
#> RS8 (.p8.) 1.214 0.085 14.216 0.000 1.274 0.644
#> RS9 (.p9.) 1.265 0.085 14.833 0.000 1.327 0.677
#> RS10 (.10.) 1.183 0.084 14.124 0.000 1.241 0.656
#> RS11 (.11.) 1.293 0.088 14.648 0.000 1.357 0.686
#> RS12 (.12.) 1.187 0.085 14.028 0.000 1.246 0.634
#> RS13 (.13.) 1.368 0.091 15.062 0.000 1.435 0.698
#> RS14 (.14.) 1.338 0.085 15.761 0.000 1.403 0.812
#>
#> Intercepts:
#> Estimate Std.Err z-value P(>|z|) Std.lv Std.all
#> .RS1 (.30.) 4.866 0.090 54.364 0.000 4.866 2.755
#> .RS2 (.31.) 4.252 0.104 40.972 0.000 4.252 2.058
#> .RS3 (.32.) 4.202 0.094 44.469 0.000 4.202 2.223
#> .RS4 (.33.) 4.498 0.107 42.235 0.000 4.498 2.155
#> .RS5 (.34.) 3.851 0.106 36.218 0.000 3.851 1.840
#> .RS6 (.35.) 5.077 0.098 51.873 0.000 5.077 2.851
#> .RS7 (.36.) 4.975 0.100 49.859 0.000 4.975 2.760
#> .RS8 (.37.) 4.404 0.100 44.026 0.000 4.404 2.225
#> .RS9 (.38.) 4.291 0.100 42.723 0.000 4.291 2.188
#> .RS10 (.39.) 4.645 0.098 47.580 0.000 4.645 2.455
#> .RS11 (.40.) 4.522 0.103 43.754 0.000 4.522 2.286
#> .RS12 (.41.) 5.006 0.099 50.590 0.000 5.006 2.547
#> .RS13 (.42.) 4.916 0.107 45.940 0.000 4.916 2.391
#> .RS14 (.43.) 4.784 0.099 48.420 0.000 4.784 2.767
#>
#> Variances:
#> Estimate Std.Err z-value P(>|z|) Std.lv Std.all
#> .RS1 2.019 0.183 11.027 0.000 2.019 0.647
#> .RS2 2.606 0.238 10.944 0.000 2.606 0.611
#> .RS3 2.342 0.212 11.046 0.000 2.342 0.655
#> .RS4 2.714 0.247 10.972 0.000 2.714 0.623
#> .RS5 2.814 0.255 11.016 0.000 2.814 0.642
#> .RS6 1.530 0.145 10.531 0.000 1.530 0.482
#> .RS7 1.480 0.142 10.416 0.000 1.480 0.455
#> .RS8 2.295 0.211 10.880 0.000 2.295 0.586
#> .RS9 2.085 0.194 10.754 0.000 2.085 0.542
#> .RS10 2.040 0.188 10.834 0.000 2.040 0.570
#> .RS11 2.074 0.194 10.712 0.000 2.074 0.530
#> .RS12 2.310 0.212 10.913 0.000 2.310 0.598
#> .RS13 2.169 0.204 10.656 0.000 2.169 0.513
#> .RS14 1.019 0.105 9.727 0.000 1.019 0.341
#> RS 1.101 0.157 7.011 0.000 1.000 1.000
#>
#> R-Square:
#> Estimate
#> RS1 0.353
#> RS2 0.389
#> RS3 0.345
#> RS4 0.377
#> RS5 0.358
#> RS6 0.518
#> RS7 0.545
#> RS8 0.414
#> RS9 0.458
#> RS10 0.430
#> RS11 0.470
#> RS12 0.402
#> RS13 0.487
#> RS14 0.659
#>
#>
#> Group 2 [Men]:
#>
#> Latent Variables:
#> Estimate Std.Err z-value P(>|z|) Std.lv Std.all
#> RS =~
#> RS1 1.000 1.228 0.680
#> RS2 (.p2.) 1.229 0.089 13.815 0.000 1.509 0.749
#> RS3 (.p3.) 1.057 0.082 12.939 0.000 1.299 0.690
#> RS4 (.p4.) 1.221 0.092 13.252 0.000 1.500 0.703
#> RS5 (.p5.) 1.193 0.092 12.939 0.000 1.466 0.683
#> RS6 (.p6.) 1.221 0.085 14.382 0.000 1.500 0.747
#> RS7 (.p7.) 1.268 0.086 14.682 0.000 1.557 0.767
#> RS8 (.p8.) 1.214 0.085 14.216 0.000 1.491 0.775
#> RS9 (.p9.) 1.265 0.085 14.833 0.000 1.554 0.814
#> RS10 (.10.) 1.183 0.084 14.124 0.000 1.453 0.761
#> RS11 (.11.) 1.293 0.088 14.648 0.000 1.588 0.794
#> RS12 (.12.) 1.187 0.085 14.028 0.000 1.458 0.763
#> RS13 (.13.) 1.368 0.091 15.062 0.000 1.680 0.825
#> RS14 (.14.) 1.338 0.085 15.761 0.000 1.643 0.837
#>
#> Intercepts:
#> Estimate Std.Err z-value P(>|z|) Std.lv Std.all
#> .RS1 (.30.) 4.866 0.090 54.364 0.000 4.866 2.693
#> .RS2 (.31.) 4.252 0.104 40.972 0.000 4.252 2.110
#> .RS3 (.32.) 4.202 0.094 44.469 0.000 4.202 2.232
#> .RS4 (.33.) 4.498 0.107 42.235 0.000 4.498 2.109
#> .RS5 (.34.) 3.851 0.106 36.218 0.000 3.851 1.794
#> .RS6 (.35.) 5.077 0.098 51.873 0.000 5.077 2.530
#> .RS7 (.36.) 4.975 0.100 49.859 0.000 4.975 2.450
#> .RS8 (.37.) 4.404 0.100 44.026 0.000 4.404 2.288
#> .RS9 (.38.) 4.291 0.100 42.723 0.000 4.291 2.248
#> .RS10 (.39.) 4.645 0.098 47.580 0.000 4.645 2.433
#> .RS11 (.40.) 4.522 0.103 43.754 0.000 4.522 2.262
#> .RS12 (.41.) 5.006 0.099 50.590 0.000 5.006 2.619
#> .RS13 (.42.) 4.916 0.107 45.940 0.000 4.916 2.415
#> .RS14 (.43.) 4.784 0.099 48.420 0.000 4.784 2.437
#> RS -0.054 0.105 -0.512 0.609 -0.044 -0.044
#>
#> Variances:
#> Estimate Std.Err z-value P(>|z|) Std.lv Std.all
#> .RS1 1.757 0.166 10.579 0.000 1.757 0.538
#> .RS2 1.784 0.172 10.350 0.000 1.784 0.439
#> .RS3 1.858 0.176 10.552 0.000 1.858 0.524
#> .RS4 2.300 0.219 10.514 0.000 2.300 0.506
#> .RS5 2.457 0.232 10.571 0.000 2.457 0.533
#> .RS6 1.779 0.172 10.361 0.000 1.779 0.442
#> .RS7 1.700 0.165 10.273 0.000 1.700 0.412
#> .RS8 1.481 0.145 10.226 0.000 1.481 0.400
#> .RS9 1.230 0.123 9.973 0.000 1.230 0.338
#> .RS10 1.533 0.149 10.296 0.000 1.533 0.421
#> .RS11 1.476 0.146 10.114 0.000 1.476 0.369
#> .RS12 1.527 0.148 10.286 0.000 1.527 0.418
#> .RS13 1.321 0.134 9.878 0.000 1.321 0.319
#> .RS14 1.156 0.118 9.778 0.000 1.156 0.300
#> RS 1.509 0.217 6.966 0.000 1.000 1.000
#>
#> R-Square:
#> Estimate
#> RS1 0.462
#> RS2 0.561
#> RS3 0.476
#> RS4 0.494
#> RS5 0.467
#> RS6 0.558
#> RS7 0.588
#> RS8 0.600
#> RS9 0.662
#> RS10 0.579
#> RS11 0.631
#> RS12 0.582
#> RS13 0.681
#> RS14 0.700Add the fit to table
table_fit[6, ] <- c("Scalar Model", round(fitmeasures(scalar.fit,
c("chisq", "df", "cfi",
"rmsea", "srmr")),3))
kable(table_fit)| Model | X2 | df | CFI | RMSEA | SRMR |
|---|---|---|---|---|---|
| Overall Model | 368.984 | 77 | 0.927 | 0.086 | 0.041 |
| Men Model | 271.457 | 77 | 0.92 | 0.102 | 0.041 |
| Women Model | 258.61 | 77 | 0.895 | 0.094 | 0.052 |
| Configural Model | 530.067 | 154 | 0.909 | 0.098 | 0.047 |
| Metric Model | 545.518 | 167 | 0.909 | 0.094 | 0.057 |
| Scalar Model | 585.327 | 180 | 0.902 | 0.094 | 0.06 |
| NA | NA | NA | NA | NA | NA |
| NA | NA | NA | NA | NA | NA |
| NA | NA | NA | NA | NA | NA |
Strict (Error) Invariance
- Are the item residuals the same?
strict.fit <- cfa(model = overall.model,
data = res.data,
meanstructure = TRUE,
group = "Sex",
group.equal = c("loadings", "intercepts", "residuals"))
summary(strict.fit,
standardized = TRUE,
rsquare = TRUE,
fit.measure = TRUE)
#> lavaan 0.6-19 ended normally after 46 iterations
#>
#> Estimator ML
#> Optimization method NLMINB
#> Number of model parameters 85
#> Number of equality constraints 41
#>
#> Number of observations per group:
#> Women 266
#> Men 244
#>
#> Model Test User Model:
#>
#> Test statistic 660.398
#> Degrees of freedom 194
#> P-value (Chi-square) 0.000
#> Test statistic for each group:
#> Women 314.816
#> Men 345.582
#>
#> Model Test Baseline Model:
#>
#> Test statistic 4328.931
#> Degrees of freedom 182
#> P-value 0.000
#>
#> User Model versus Baseline Model:
#>
#> Comparative Fit Index (CFI) 0.888
#> Tucker-Lewis Index (TLI) 0.894
#>
#> Loglikelihood and Information Criteria:
#>
#> Loglikelihood user model (H0) -13047.576
#> Loglikelihood unrestricted model (H1) -12717.377
#>
#> Akaike (AIC) 26183.153
#> Bayesian (BIC) 26369.467
#> Sample-size adjusted Bayesian (SABIC) 26229.805
#>
#> Root Mean Square Error of Approximation:
#>
#> RMSEA 0.097
#> 90 Percent confidence interval - lower 0.089
#> 90 Percent confidence interval - upper 0.105
#> P-value H_0: RMSEA <= 0.050 0.000
#> P-value H_0: RMSEA >= 0.080 1.000
#>
#> Standardized Root Mean Square Residual:
#>
#> SRMR 0.062
#>
#> Parameter Estimates:
#>
#> Standard errors Standard
#> Information Expected
#> Information saturated (h1) model Structured
#>
#>
#> Group 1 [Women]:
#>
#> Latent Variables:
#> Estimate Std.Err z-value P(>|z|) Std.lv Std.all
#> RS =~
#> RS1 1.000 1.052 0.608
#> RS2 (.p2.) 1.229 0.091 13.545 0.000 1.292 0.657
#> RS3 (.p3.) 1.064 0.083 12.817 0.000 1.119 0.612
#> RS4 (.p4.) 1.229 0.093 13.156 0.000 1.293 0.632
#> RS5 (.p5.) 1.201 0.093 12.851 0.000 1.262 0.614
#> RS6 (.p6.) 1.217 0.085 14.274 0.000 1.280 0.705
#> RS7 (.p7.) 1.262 0.087 14.567 0.000 1.327 0.725
#> RS8 (.p8.) 1.206 0.087 13.852 0.000 1.269 0.677
#> RS9 (.p9.) 1.270 0.088 14.473 0.000 1.335 0.718
#> RS10 (.10.) 1.192 0.085 13.957 0.000 1.253 0.684
#> RS11 (.11.) 1.315 0.090 14.535 0.000 1.383 0.722
#> RS12 (.12.) 1.156 0.085 13.524 0.000 1.216 0.656
#> RS13 (.13.) 1.356 0.093 14.656 0.000 1.426 0.731
#> RS14 (.14.) 1.334 0.085 15.610 0.000 1.402 0.800
#>
#> Intercepts:
#> Estimate Std.Err z-value P(>|z|) Std.lv Std.all
#> .RS1 (.30.) 4.874 0.090 54.448 0.000 4.874 2.817
#> .RS2 (.31.) 4.249 0.104 40.833 0.000 4.249 2.160
#> .RS3 (.32.) 4.190 0.095 44.193 0.000 4.190 2.291
#> .RS4 (.33.) 4.482 0.107 41.915 0.000 4.482 2.193
#> .RS5 (.34.) 3.838 0.107 35.963 0.000 3.838 1.866
#> .RS6 (.35.) 5.068 0.098 51.613 0.000 5.068 2.791
#> .RS7 (.36.) 4.969 0.100 49.707 0.000 4.969 2.713
#> .RS8 (.37.) 4.381 0.100 43.790 0.000 4.381 2.337
#> .RS9 (.38.) 4.265 0.101 42.167 0.000 4.265 2.295
#> .RS10 (.39.) 4.652 0.098 47.397 0.000 4.652 2.538
#> .RS11 (.40.) 4.519 0.104 43.296 0.000 4.519 2.361
#> .RS12 (.41.) 5.035 0.098 51.359 0.000 5.035 2.715
#> .RS13 (.42.) 4.928 0.107 46.139 0.000 4.928 2.526
#> .RS14 (.43.) 4.783 0.099 48.219 0.000 4.783 2.728
#>
#> Variances:
#> Estimate Std.Err z-value P(>|z|) Std.lv Std.all
#> .RS1 (.15.) 1.887 0.124 15.241 0.000 1.887 0.631
#> .RS2 (.16.) 2.200 0.146 15.025 0.000 2.200 0.568
#> .RS3 (.17.) 2.094 0.138 15.226 0.000 2.094 0.626
#> .RS4 (.18.) 2.507 0.166 15.141 0.000 2.507 0.600
#> .RS5 (.19.) 2.638 0.173 15.218 0.000 2.638 0.623
#> .RS6 (.20.) 1.660 0.113 14.742 0.000 1.660 0.503
#> .RS7 (.21.) 1.593 0.109 14.593 0.000 1.593 0.475
#> .RS8 (.22.) 1.905 0.128 14.918 0.000 1.905 0.542
#> .RS9 (.23.) 1.673 0.114 14.643 0.000 1.673 0.484
#> .RS10 (.24.) 1.789 0.120 14.878 0.000 1.789 0.533
#> .RS11 (.25.) 1.752 0.120 14.610 0.000 1.752 0.478
#> .RS12 (.26.) 1.961 0.130 15.032 0.000 1.961 0.570
#> .RS13 (.27.) 1.773 0.122 14.542 0.000 1.773 0.466
#> .RS14 (.28.) 1.106 0.080 13.754 0.000 1.106 0.360
#> RS 1.106 0.158 6.990 0.000 1.000 1.000
#>
#> R-Square:
#> Estimate
#> RS1 0.369
#> RS2 0.432
#> RS3 0.374
#> RS4 0.400
#> RS5 0.377
#> RS6 0.497
#> RS7 0.525
#> RS8 0.458
#> RS9 0.516
#> RS10 0.467
#> RS11 0.522
#> RS12 0.430
#> RS13 0.534
#> RS14 0.640
#>
#>
#> Group 2 [Men]:
#>
#> Latent Variables:
#> Estimate Std.Err z-value P(>|z|) Std.lv Std.all
#> RS =~
#> RS1 1.000 1.222 0.665
#> RS2 (.p2.) 1.229 0.091 13.545 0.000 1.502 0.711
#> RS3 (.p3.) 1.064 0.083 12.817 0.000 1.300 0.668
#> RS4 (.p4.) 1.229 0.093 13.156 0.000 1.502 0.688
#> RS5 (.p5.) 1.201 0.093 12.851 0.000 1.467 0.670
#> RS6 (.p6.) 1.217 0.085 14.274 0.000 1.487 0.756
#> RS7 (.p7.) 1.262 0.087 14.567 0.000 1.542 0.774
#> RS8 (.p8.) 1.206 0.087 13.852 0.000 1.474 0.730
#> RS9 (.p9.) 1.270 0.088 14.473 0.000 1.552 0.768
#> RS10 (.10.) 1.192 0.085 13.957 0.000 1.456 0.736
#> RS11 (.11.) 1.315 0.090 14.535 0.000 1.607 0.772
#> RS12 (.12.) 1.156 0.085 13.524 0.000 1.413 0.710
#> RS13 (.13.) 1.356 0.093 14.656 0.000 1.657 0.780
#> RS14 (.14.) 1.334 0.085 15.610 0.000 1.630 0.840
#>
#> Intercepts:
#> Estimate Std.Err z-value P(>|z|) Std.lv Std.all
#> .RS1 (.30.) 4.874 0.090 54.448 0.000 4.874 2.651
#> .RS2 (.31.) 4.249 0.104 40.833 0.000 4.249 2.013
#> .RS3 (.32.) 4.190 0.095 44.193 0.000 4.190 2.154
#> .RS4 (.33.) 4.482 0.107 41.915 0.000 4.482 2.054
#> .RS5 (.34.) 3.838 0.107 35.963 0.000 3.838 1.754
#> .RS6 (.35.) 5.068 0.098 51.613 0.000 5.068 2.576
#> .RS7 (.36.) 4.969 0.100 49.707 0.000 4.969 2.493
#> .RS8 (.37.) 4.381 0.100 43.790 0.000 4.381 2.170
#> .RS9 (.38.) 4.265 0.101 42.167 0.000 4.265 2.112
#> .RS10 (.39.) 4.652 0.098 47.397 0.000 4.652 2.353
#> .RS11 (.40.) 4.519 0.104 43.296 0.000 4.519 2.171
#> .RS12 (.41.) 5.035 0.098 51.359 0.000 5.035 2.531
#> .RS13 (.42.) 4.928 0.107 46.139 0.000 4.928 2.318
#> .RS14 (.43.) 4.783 0.099 48.219 0.000 4.783 2.466
#> RS -0.053 0.105 -0.504 0.614 -0.043 -0.043
#>
#> Variances:
#> Estimate Std.Err z-value P(>|z|) Std.lv Std.all
#> .RS1 (.15.) 1.887 0.124 15.241 0.000 1.887 0.558
#> .RS2 (.16.) 2.200 0.146 15.025 0.000 2.200 0.494
#> .RS3 (.17.) 2.094 0.138 15.226 0.000 2.094 0.553
#> .RS4 (.18.) 2.507 0.166 15.141 0.000 2.507 0.526
#> .RS5 (.19.) 2.638 0.173 15.218 0.000 2.638 0.551
#> .RS6 (.20.) 1.660 0.113 14.742 0.000 1.660 0.429
#> .RS7 (.21.) 1.593 0.109 14.593 0.000 1.593 0.401
#> .RS8 (.22.) 1.905 0.128 14.918 0.000 1.905 0.467
#> .RS9 (.23.) 1.673 0.114 14.643 0.000 1.673 0.410
#> .RS10 (.24.) 1.789 0.120 14.878 0.000 1.789 0.458
#> .RS11 (.25.) 1.752 0.120 14.610 0.000 1.752 0.404
#> .RS12 (.26.) 1.961 0.130 15.032 0.000 1.961 0.496
#> .RS13 (.27.) 1.773 0.122 14.542 0.000 1.773 0.392
#> .RS14 (.28.) 1.106 0.080 13.754 0.000 1.106 0.294
#> RS 1.493 0.216 6.917 0.000 1.000 1.000
#>
#> R-Square:
#> Estimate
#> RS1 0.442
#> RS2 0.506
#> RS3 0.447
#> RS4 0.474
#> RS5 0.449
#> RS6 0.571
#> RS7 0.599
#> RS8 0.533
#> RS9 0.590
#> RS10 0.542
#> RS11 0.596
#> RS12 0.504
#> RS13 0.608
#> RS14 0.706Add the fit to table
table_fit[7, ] <- c("Strict Model", round(fitmeasures(strict.fit,
c("chisq", "df", "cfi",
"rmsea", "srmr")),3))
kable(table_fit)| Model | X2 | df | CFI | RMSEA | SRMR |
|---|---|---|---|---|---|
| Overall Model | 368.984 | 77 | 0.927 | 0.086 | 0.041 |
| Men Model | 271.457 | 77 | 0.92 | 0.102 | 0.041 |
| Women Model | 258.61 | 77 | 0.895 | 0.094 | 0.052 |
| Configural Model | 530.067 | 154 | 0.909 | 0.098 | 0.047 |
| Metric Model | 545.518 | 167 | 0.909 | 0.094 | 0.057 |
| Scalar Model | 585.327 | 180 | 0.902 | 0.094 | 0.06 |
| Strict Model | 660.398 | 194 | 0.888 | 0.097 | 0.062 |
| NA | NA | NA | NA | NA | NA |
| NA | NA | NA | NA | NA | NA |
Partial Invariance
- We can see in this last step that we have a difference in models based on change in CFI.
- Now, we have to figure out where the problem is and update our model to fix that problem.
- You would only look for problems in the step you are in.
Partial Invariance
- Figure out which level you need:
- metric
=~for loadings - scalar
~1for intercepts - strict
~~for variances
- metric
- Change each item one at a time and note the changes
Partial Invariance
##write out partial codes
partial_syntax <- paste(colnames(res.data)[3:16], #all the columns
"~~", #residuals
colnames(res.data)[3:16]) #all columns again
partial_syntax
#> [1] "RS1 ~~ RS1" "RS2 ~~ RS2" "RS3 ~~ RS3" "RS4 ~~ RS4" "RS5 ~~ RS5"
#> [6] "RS6 ~~ RS6" "RS7 ~~ RS7" "RS8 ~~ RS8" "RS9 ~~ RS9" "RS10 ~~ RS10"
#> [11] "RS11 ~~ RS11" "RS12 ~~ RS12" "RS13 ~~ RS13" "RS14 ~~ RS14"
CFI_list <- 1:length(partial_syntax)
names(CFI_list) <- partial_syntax
for (i in 1:length(partial_syntax)){
temp <- cfa(model = overall.model,
data = res.data,
meanstructure = TRUE,
group = "Sex",
group.equal = c("loadings", "intercepts", "residuals"),
group.partial = partial_syntax[i])
CFI_list[i] <- fitmeasures(temp, "cfi")
}
CFI_list
#> RS1 ~~ RS1 RS2 ~~ RS2 RS3 ~~ RS3 RS4 ~~ RS4 RS5 ~~ RS5 RS6 ~~ RS6
#> 0.8877040 0.8892794 0.8881315 0.8876596 0.8875493 0.8874662
#> RS7 ~~ RS7 RS8 ~~ RS8 RS9 ~~ RS9 RS10 ~~ RS10 RS11 ~~ RS11 RS12 ~~ RS12
#> 0.8873667 0.8897416 0.8906278 0.8882753 0.8888421 0.8896339
#> RS13 ~~ RS13 RS14 ~~ RS14
#> 0.8905766 0.8873834
which.max(CFI_list)
#> RS9 ~~ RS9
#> 9Free up those paramers!
strict.fit2 <- cfa(model = overall.model,
data = res.data,
meanstructure = TRUE,
group = "Sex",
group.equal = c("loadings", "intercepts", "residuals"),
group.partial = c("RS9 ~~ RS9"))
summary(strict.fit2,
standardized = TRUE,
rsquare = TRUE,
fit.measure = TRUE)
#> lavaan 0.6-19 ended normally after 48 iterations
#>
#> Estimator ML
#> Optimization method NLMINB
#> Number of model parameters 85
#> Number of equality constraints 40
#>
#> Number of observations per group:
#> Women 266
#> Men 244
#>
#> Model Test User Model:
#>
#> Test statistic 646.559
#> Degrees of freedom 193
#> P-value (Chi-square) 0.000
#> Test statistic for each group:
#> Women 310.363
#> Men 336.196
#>
#> Model Test Baseline Model:
#>
#> Test statistic 4328.931
#> Degrees of freedom 182
#> P-value 0.000
#>
#> User Model versus Baseline Model:
#>
#> Comparative Fit Index (CFI) 0.891
#> Tucker-Lewis Index (TLI) 0.897
#>
#> Loglikelihood and Information Criteria:
#>
#> Loglikelihood user model (H0) -13040.657
#> Loglikelihood unrestricted model (H1) -12717.377
#>
#> Akaike (AIC) 26171.314
#> Bayesian (BIC) 26361.863
#> Sample-size adjusted Bayesian (SABIC) 26219.026
#>
#> Root Mean Square Error of Approximation:
#>
#> RMSEA 0.096
#> 90 Percent confidence interval - lower 0.088
#> 90 Percent confidence interval - upper 0.104
#> P-value H_0: RMSEA <= 0.050 0.000
#> P-value H_0: RMSEA >= 0.080 0.999
#>
#> Standardized Root Mean Square Residual:
#>
#> SRMR 0.062
#>
#> Parameter Estimates:
#>
#> Standard errors Standard
#> Information Expected
#> Information saturated (h1) model Structured
#>
#>
#> Group 1 [Women]:
#>
#> Latent Variables:
#> Estimate Std.Err z-value P(>|z|) Std.lv Std.all
#> RS =~
#> RS1 1.000 1.050 0.607
#> RS2 (.p2.) 1.229 0.091 13.526 0.000 1.290 0.656
#> RS3 (.p3.) 1.064 0.083 12.806 0.000 1.117 0.611
#> RS4 (.p4.) 1.232 0.094 13.161 0.000 1.293 0.633
#> RS5 (.p5.) 1.200 0.094 12.829 0.000 1.260 0.612
#> RS6 (.p6.) 1.218 0.085 14.264 0.000 1.279 0.704
#> RS7 (.p7.) 1.263 0.087 14.550 0.000 1.325 0.724
#> RS8 (.p8.) 1.207 0.087 13.840 0.000 1.267 0.676
#> RS9 (.p9.) 1.269 0.086 14.706 0.000 1.332 0.679
#> RS10 (.10.) 1.194 0.086 13.965 0.000 1.254 0.684
#> RS11 (.11.) 1.313 0.091 14.497 0.000 1.379 0.720
#> RS12 (.12.) 1.160 0.086 13.546 0.000 1.218 0.657
#> RS13 (.13.) 1.359 0.093 14.659 0.000 1.427 0.732
#> RS14 (.14.) 1.334 0.086 15.592 0.000 1.401 0.799
#>
#> Intercepts:
#> Estimate Std.Err z-value P(>|z|) Std.lv Std.all
#> .RS1 (.30.) 4.874 0.089 54.484 0.000 4.874 2.818
#> .RS2 (.31.) 4.249 0.104 40.863 0.000 4.249 2.160
#> .RS3 (.32.) 4.190 0.095 44.218 0.000 4.190 2.291
#> .RS4 (.33.) 4.482 0.107 41.924 0.000 4.482 2.194
#> .RS5 (.34.) 3.838 0.107 35.990 0.000 3.838 1.866
#> .RS6 (.35.) 5.068 0.098 51.642 0.000 5.068 2.792
#> .RS7 (.36.) 4.969 0.100 49.744 0.000 4.969 2.714
#> .RS8 (.37.) 4.381 0.100 43.816 0.000 4.381 2.338
#> .RS9 (.38.) 4.290 0.101 42.586 0.000 4.290 2.187
#> .RS10 (.39.) 4.652 0.098 47.405 0.000 4.652 2.539
#> .RS11 (.40.) 4.519 0.104 43.349 0.000 4.519 2.361
#> .RS12 (.41.) 5.035 0.098 51.351 0.000 5.035 2.717
#> .RS13 (.42.) 4.928 0.107 46.152 0.000 4.928 2.527
#> .RS14 (.43.) 4.783 0.099 48.258 0.000 4.783 2.730
#>
#> Variances:
#> Estimate Std.Err z-value P(>|z|) Std.lv Std.all
#> .RS1 (.15.) 1.889 0.124 15.247 0.000 1.889 0.632
#> .RS2 (.16.) 2.203 0.147 15.033 0.000 2.203 0.570
#> .RS3 (.17.) 2.095 0.138 15.231 0.000 2.095 0.627
#> .RS4 (.18.) 2.502 0.165 15.141 0.000 2.502 0.599
#> .RS5 (.19.) 2.643 0.174 15.226 0.000 2.643 0.625
#> .RS6 (.20.) 1.660 0.113 14.748 0.000 1.660 0.504
#> .RS7 (.21.) 1.595 0.109 14.603 0.000 1.595 0.476
#> .RS8 (.22.) 1.905 0.128 14.924 0.000 1.905 0.543
#> .RS9 2.072 0.192 10.787 0.000 2.072 0.539
#> .RS10 (.24.) 1.783 0.120 14.876 0.000 1.783 0.531
#> .RS11 (.25.) 1.762 0.120 14.631 0.000 1.762 0.481
#> .RS12 (.26.) 1.951 0.130 15.027 0.000 1.951 0.568
#> .RS13 (.27.) 1.768 0.122 14.541 0.000 1.768 0.465
#> .RS14 (.28.) 1.108 0.080 13.770 0.000 1.108 0.361
#> RS 1.102 0.158 6.983 0.000 1.000 1.000
#>
#> R-Square:
#> Estimate
#> RS1 0.368
#> RS2 0.430
#> RS3 0.373
#> RS4 0.401
#> RS5 0.375
#> RS6 0.496
#> RS7 0.524
#> RS8 0.457
#> RS9 0.461
#> RS10 0.469
#> RS11 0.519
#> RS12 0.432
#> RS13 0.535
#> RS14 0.639
#>
#>
#> Group 2 [Men]:
#>
#> Latent Variables:
#> Estimate Std.Err z-value P(>|z|) Std.lv Std.all
#> RS =~
#> RS1 1.000 1.222 0.664
#> RS2 (.p2.) 1.229 0.091 13.526 0.000 1.501 0.711
#> RS3 (.p3.) 1.064 0.083 12.806 0.000 1.300 0.668
#> RS4 (.p4.) 1.232 0.094 13.161 0.000 1.505 0.689
#> RS5 (.p5.) 1.200 0.094 12.829 0.000 1.466 0.670
#> RS6 (.p6.) 1.218 0.085 14.264 0.000 1.488 0.756
#> RS7 (.p7.) 1.263 0.087 14.550 0.000 1.543 0.774
#> RS8 (.p8.) 1.207 0.087 13.840 0.000 1.475 0.730
#> RS9 (.p9.) 1.269 0.086 14.706 0.000 1.551 0.813
#> RS10 (.10.) 1.194 0.086 13.965 0.000 1.459 0.738
#> RS11 (.11.) 1.313 0.091 14.497 0.000 1.605 0.771
#> RS12 (.12.) 1.160 0.086 13.546 0.000 1.418 0.712
#> RS13 (.13.) 1.359 0.093 14.659 0.000 1.661 0.781
#> RS14 (.14.) 1.334 0.086 15.592 0.000 1.630 0.840
#>
#> Intercepts:
#> Estimate Std.Err z-value P(>|z|) Std.lv Std.all
#> .RS1 (.30.) 4.874 0.089 54.484 0.000 4.874 2.650
#> .RS2 (.31.) 4.249 0.104 40.863 0.000 4.249 2.012
#> .RS3 (.32.) 4.190 0.095 44.218 0.000 4.190 2.153
#> .RS4 (.33.) 4.482 0.107 41.924 0.000 4.482 2.053
#> .RS5 (.34.) 3.838 0.107 35.990 0.000 3.838 1.753
#> .RS6 (.35.) 5.068 0.098 51.642 0.000 5.068 2.575
#> .RS7 (.36.) 4.969 0.100 49.744 0.000 4.969 2.492
#> .RS8 (.37.) 4.381 0.100 43.816 0.000 4.381 2.169
#> .RS9 (.38.) 4.290 0.101 42.586 0.000 4.290 2.247
#> .RS10 (.39.) 4.652 0.098 47.405 0.000 4.652 2.351
#> .RS11 (.40.) 4.519 0.104 43.349 0.000 4.519 2.170
#> .RS12 (.41.) 5.035 0.098 51.351 0.000 5.035 2.530
#> .RS13 (.42.) 4.928 0.107 46.152 0.000 4.928 2.317
#> .RS14 (.43.) 4.783 0.099 48.258 0.000 4.783 2.465
#> RS -0.053 0.105 -0.503 0.615 -0.043 -0.043
#>
#> Variances:
#> Estimate Std.Err z-value P(>|z|) Std.lv Std.all
#> .RS1 (.15.) 1.889 0.124 15.247 0.000 1.889 0.559
#> .RS2 (.16.) 2.203 0.147 15.033 0.000 2.203 0.494
#> .RS3 (.17.) 2.095 0.138 15.231 0.000 2.095 0.553
#> .RS4 (.18.) 2.502 0.165 15.141 0.000 2.502 0.525
#> .RS5 (.19.) 2.643 0.174 15.226 0.000 2.643 0.551
#> .RS6 (.20.) 1.660 0.113 14.748 0.000 1.660 0.428
#> .RS7 (.21.) 1.595 0.109 14.603 0.000 1.595 0.401
#> .RS8 (.22.) 1.905 0.128 14.924 0.000 1.905 0.467
#> .RS9 1.238 0.125 9.864 0.000 1.238 0.340
#> .RS10 (.24.) 1.783 0.120 14.876 0.000 1.783 0.456
#> .RS11 (.25.) 1.762 0.120 14.631 0.000 1.762 0.406
#> .RS12 (.26.) 1.951 0.130 15.027 0.000 1.951 0.493
#> .RS13 (.27.) 1.768 0.122 14.541 0.000 1.768 0.391
#> .RS14 (.28.) 1.108 0.080 13.770 0.000 1.108 0.294
#> RS 1.493 0.216 6.911 0.000 1.000 1.000
#>
#> R-Square:
#> Estimate
#> RS1 0.441
#> RS2 0.506
#> RS3 0.447
#> RS4 0.475
#> RS5 0.449
#> RS6 0.572
#> RS7 0.599
#> RS8 0.533
#> RS9 0.660
#> RS10 0.544
#> RS11 0.594
#> RS12 0.507
#> RS13 0.609
#> RS14 0.706Add the fit to table
table_fit[8, ] <- c("Strict Model RS9", round(fitmeasures(strict.fit2,
c("chisq", "df", "cfi",
"rmsea", "srmr")),3))
kable(table_fit)| Model | X2 | df | CFI | RMSEA | SRMR |
|---|---|---|---|---|---|
| Overall Model | 368.984 | 77 | 0.927 | 0.086 | 0.041 |
| Men Model | 271.457 | 77 | 0.92 | 0.102 | 0.041 |
| Women Model | 258.61 | 77 | 0.895 | 0.094 | 0.052 |
| Configural Model | 530.067 | 154 | 0.909 | 0.098 | 0.047 |
| Metric Model | 545.518 | 167 | 0.909 | 0.094 | 0.057 |
| Scalar Model | 585.327 | 180 | 0.902 | 0.094 | 0.06 |
| Strict Model | 660.398 | 194 | 0.888 | 0.097 | 0.062 |
| Strict Model RS9 | 646.559 | 193 | 0.891 | 0.096 | 0.062 |
| NA | NA | NA | NA | NA | NA |
Find one more free parameter
- We want to see if we can get up to .902 - .01 = .892 for our CFI.
for (i in 1:length(partial_syntax)){
temp <- cfa(model = overall.model,
data = res.data,
meanstructure = TRUE,
group = "Sex",
group.equal = c("loadings", "intercepts", "residuals"),
group.partial = c("RS9 ~~ RS9", partial_syntax[i]))
CFI_list[i] <- fitmeasures(temp, "cfi")
}
CFI_list
#> RS1 ~~ RS1 RS2 ~~ RS2 RS3 ~~ RS3 RS4 ~~ RS4 RS5 ~~ RS5 RS6 ~~ RS6
#> 0.8907350 0.8923563 0.8911657 0.8907125 0.8906552 0.8905857
#> RS7 ~~ RS7 RS8 ~~ RS8 RS9 ~~ RS9 RS10 ~~ RS10 RS11 ~~ RS11 RS12 ~~ RS12
#> 0.8904937 0.8930016 0.8906278 0.8914713 0.8919005 0.8927904
#> RS13 ~~ RS13 RS14 ~~ RS14
#> 0.8936296 0.8904971
which.max(CFI_list)
#> RS13 ~~ RS13
#> 13Add one more free parameter
strict.fit3 <- cfa(model = overall.model,
data = res.data,
meanstructure = TRUE,
group = "Sex",
group.equal = c("loadings", "intercepts", "residuals"),
group.partial = c("RS9 ~~ RS9", "RS13 ~~ RS13"))
summary(strict.fit3,
standardized = TRUE,
rsquare = TRUE,
fit.measure = TRUE)
#> lavaan 0.6-19 ended normally after 44 iterations
#>
#> Estimator ML
#> Optimization method NLMINB
#> Number of model parameters 85
#> Number of equality constraints 39
#>
#> Number of observations per group:
#> Women 266
#> Men 244
#>
#> Model Test User Model:
#>
#> Test statistic 633.111
#> Degrees of freedom 192
#> P-value (Chi-square) 0.000
#> Test statistic for each group:
#> Women 305.696
#> Men 327.415
#>
#> Model Test Baseline Model:
#>
#> Test statistic 4328.931
#> Degrees of freedom 182
#> P-value 0.000
#>
#> User Model versus Baseline Model:
#>
#> Comparative Fit Index (CFI) 0.894
#> Tucker-Lewis Index (TLI) 0.899
#>
#> Loglikelihood and Information Criteria:
#>
#> Loglikelihood user model (H0) -13033.933
#> Loglikelihood unrestricted model (H1) -12717.377
#>
#> Akaike (AIC) 26159.866
#> Bayesian (BIC) 26354.649
#> Sample-size adjusted Bayesian (SABIC) 26208.638
#>
#> Root Mean Square Error of Approximation:
#>
#> RMSEA 0.095
#> 90 Percent confidence interval - lower 0.087
#> 90 Percent confidence interval - upper 0.103
#> P-value H_0: RMSEA <= 0.050 0.000
#> P-value H_0: RMSEA >= 0.080 0.999
#>
#> Standardized Root Mean Square Residual:
#>
#> SRMR 0.062
#>
#> Parameter Estimates:
#>
#> Standard errors Standard
#> Information Expected
#> Information saturated (h1) model Structured
#>
#>
#> Group 1 [Women]:
#>
#> Latent Variables:
#> Estimate Std.Err z-value P(>|z|) Std.lv Std.all
#> RS =~
#> RS1 1.000 1.050 0.607
#> RS2 (.p2.) 1.230 0.091 13.554 0.000 1.291 0.657
#> RS3 (.p3.) 1.061 0.083 12.794 0.000 1.114 0.609
#> RS4 (.p4.) 1.227 0.093 13.133 0.000 1.287 0.630
#> RS5 (.p5.) 1.201 0.093 12.853 0.000 1.260 0.613
#> RS6 (.p6.) 1.217 0.085 14.280 0.000 1.278 0.704
#> RS7 (.p7.) 1.262 0.087 14.571 0.000 1.325 0.724
#> RS8 (.p8.) 1.208 0.087 13.872 0.000 1.268 0.677
#> RS9 (.p9.) 1.269 0.086 14.727 0.000 1.332 0.680
#> RS10 (.10.) 1.192 0.085 13.961 0.000 1.251 0.683
#> RS11 (.11.) 1.310 0.090 14.490 0.000 1.375 0.719
#> RS12 (.12.) 1.162 0.086 13.583 0.000 1.220 0.658
#> RS13 (.13.) 1.372 0.092 14.962 0.000 1.440 0.698
#> RS14 (.14.) 1.334 0.085 15.613 0.000 1.400 0.799
#>
#> Intercepts:
#> Estimate Std.Err z-value P(>|z|) Std.lv Std.all
#> .RS1 (.30.) 4.874 0.089 54.505 0.000 4.874 2.819
#> .RS2 (.31.) 4.249 0.104 40.874 0.000 4.249 2.162
#> .RS3 (.32.) 4.190 0.095 44.263 0.000 4.190 2.292
#> .RS4 (.33.) 4.482 0.107 41.983 0.000 4.482 2.194
#> .RS5 (.34.) 3.838 0.107 36.001 0.000 3.838 1.867
#> .RS6 (.35.) 5.068 0.098 51.674 0.000 5.068 2.793
#> .RS7 (.36.) 4.969 0.100 49.770 0.000 4.969 2.716
#> .RS8 (.37.) 4.382 0.100 43.826 0.000 4.382 2.340
#> .RS9 (.38.) 4.290 0.101 42.614 0.000 4.290 2.189
#> .RS10 (.39.) 4.652 0.098 47.454 0.000 4.652 2.540
#> .RS11 (.40.) 4.520 0.104 43.401 0.000 4.520 2.362
#> .RS12 (.41.) 5.035 0.098 51.354 0.000 5.035 2.718
#> .RS13 (.42.) 4.915 0.107 45.827 0.000 4.915 2.382
#> .RS14 (.43.) 4.783 0.099 48.290 0.000 4.783 2.732
#>
#> Variances:
#> Estimate Std.Err z-value P(>|z|) Std.lv Std.all
#> .RS1 (.15.) 1.888 0.124 15.250 0.000 1.888 0.632
#> .RS2 (.16.) 2.198 0.146 15.035 0.000 2.198 0.569
#> .RS3 (.17.) 2.101 0.138 15.242 0.000 2.101 0.629
#> .RS4 (.18.) 2.516 0.166 15.158 0.000 2.516 0.603
#> .RS5 (.19.) 2.639 0.173 15.228 0.000 2.639 0.624
#> .RS6 (.20.) 1.659 0.112 14.755 0.000 1.659 0.504
#> .RS7 (.21.) 1.593 0.109 14.609 0.000 1.593 0.476
#> .RS8 (.22.) 1.899 0.127 14.925 0.000 1.899 0.541
#> .RS9 2.066 0.192 10.773 0.000 2.066 0.538
#> .RS10 (.24.) 1.789 0.120 14.891 0.000 1.789 0.534
#> .RS11 (.25.) 1.771 0.121 14.652 0.000 1.771 0.484
#> .RS12 (.26.) 1.944 0.129 15.025 0.000 1.944 0.566
#> .RS13 2.184 0.204 10.693 0.000 2.184 0.513
#> .RS14 (.28.) 1.106 0.080 13.781 0.000 1.106 0.361
#> RS 1.101 0.158 6.989 0.000 1.000 1.000
#>
#> R-Square:
#> Estimate
#> RS1 0.368
#> RS2 0.431
#> RS3 0.371
#> RS4 0.397
#> RS5 0.376
#> RS6 0.496
#> RS7 0.524
#> RS8 0.459
#> RS9 0.462
#> RS10 0.466
#> RS11 0.516
#> RS12 0.434
#> RS13 0.487
#> RS14 0.639
#>
#>
#> Group 2 [Men]:
#>
#> Latent Variables:
#> Estimate Std.Err z-value P(>|z|) Std.lv Std.all
#> RS =~
#> RS1 1.000 1.224 0.665
#> RS2 (.p2.) 1.230 0.091 13.554 0.000 1.505 0.712
#> RS3 (.p3.) 1.061 0.083 12.794 0.000 1.299 0.667
#> RS4 (.p4.) 1.227 0.093 13.133 0.000 1.501 0.687
#> RS5 (.p5.) 1.201 0.093 12.853 0.000 1.469 0.671
#> RS6 (.p6.) 1.217 0.085 14.280 0.000 1.490 0.756
#> RS7 (.p7.) 1.262 0.087 14.571 0.000 1.545 0.774
#> RS8 (.p8.) 1.208 0.087 13.872 0.000 1.478 0.731
#> RS9 (.p9.) 1.269 0.086 14.727 0.000 1.553 0.813
#> RS10 (.10.) 1.192 0.085 13.961 0.000 1.458 0.737
#> RS11 (.11.) 1.310 0.090 14.490 0.000 1.603 0.769
#> RS12 (.12.) 1.162 0.086 13.583 0.000 1.422 0.714
#> RS13 (.13.) 1.372 0.092 14.962 0.000 1.679 0.826
#> RS14 (.14.) 1.334 0.085 15.613 0.000 1.632 0.841
#>
#> Intercepts:
#> Estimate Std.Err z-value P(>|z|) Std.lv Std.all
#> .RS1 (.30.) 4.874 0.089 54.505 0.000 4.874 2.649
#> .RS2 (.31.) 4.249 0.104 40.874 0.000 4.249 2.012
#> .RS3 (.32.) 4.190 0.095 44.263 0.000 4.190 2.153
#> .RS4 (.33.) 4.482 0.107 41.983 0.000 4.482 2.052
#> .RS5 (.34.) 3.838 0.107 36.001 0.000 3.838 1.753
#> .RS6 (.35.) 5.068 0.098 51.674 0.000 5.068 2.574
#> .RS7 (.36.) 4.969 0.100 49.770 0.000 4.969 2.491
#> .RS8 (.37.) 4.382 0.100 43.826 0.000 4.382 2.168
#> .RS9 (.38.) 4.290 0.101 42.614 0.000 4.290 2.246
#> .RS10 (.39.) 4.652 0.098 47.454 0.000 4.652 2.351
#> .RS11 (.40.) 4.520 0.104 43.401 0.000 4.520 2.169
#> .RS12 (.41.) 5.035 0.098 51.354 0.000 5.035 2.528
#> .RS13 (.42.) 4.915 0.107 45.827 0.000 4.915 2.419
#> .RS14 (.43.) 4.783 0.099 48.290 0.000 4.783 2.463
#> RS -0.053 0.105 -0.507 0.612 -0.043 -0.043
#>
#> Variances:
#> Estimate Std.Err z-value P(>|z|) Std.lv Std.all
#> .RS1 (.15.) 1.888 0.124 15.250 0.000 1.888 0.558
#> .RS2 (.16.) 2.198 0.146 15.035 0.000 2.198 0.493
#> .RS3 (.17.) 2.101 0.138 15.242 0.000 2.101 0.555
#> .RS4 (.18.) 2.516 0.166 15.158 0.000 2.516 0.528
#> .RS5 (.19.) 2.639 0.173 15.228 0.000 2.639 0.550
#> .RS6 (.20.) 1.659 0.112 14.755 0.000 1.659 0.428
#> .RS7 (.21.) 1.593 0.109 14.609 0.000 1.593 0.400
#> .RS8 (.22.) 1.899 0.127 14.925 0.000 1.899 0.465
#> .RS9 1.239 0.125 9.900 0.000 1.239 0.339
#> .RS10 (.24.) 1.789 0.120 14.891 0.000 1.789 0.457
#> .RS11 (.25.) 1.771 0.121 14.652 0.000 1.771 0.408
#> .RS12 (.26.) 1.944 0.129 15.025 0.000 1.944 0.490
#> .RS13 1.310 0.134 9.779 0.000 1.310 0.317
#> .RS14 (.28.) 1.106 0.080 13.781 0.000 1.106 0.294
#> RS 1.497 0.216 6.917 0.000 1.000 1.000
#>
#> R-Square:
#> Estimate
#> RS1 0.442
#> RS2 0.507
#> RS3 0.445
#> RS4 0.472
#> RS5 0.450
#> RS6 0.572
#> RS7 0.600
#> RS8 0.535
#> RS9 0.661
#> RS10 0.543
#> RS11 0.592
#> RS12 0.510
#> RS13 0.683
#> RS14 0.706Partial Invariance Met!
table_fit[9, ] <- c("Strict Model RS9 + 13", round(fitmeasures(strict.fit3,
c("chisq", "df", "cfi",
"rmsea", "srmr")),3))
kable(table_fit)| Model | X2 | df | CFI | RMSEA | SRMR |
|---|---|---|---|---|---|
| Overall Model | 368.984 | 77 | 0.927 | 0.086 | 0.041 |
| Men Model | 271.457 | 77 | 0.92 | 0.102 | 0.041 |
| Women Model | 258.61 | 77 | 0.895 | 0.094 | 0.052 |
| Configural Model | 530.067 | 154 | 0.909 | 0.098 | 0.047 |
| Metric Model | 545.518 | 167 | 0.909 | 0.094 | 0.057 |
| Scalar Model | 585.327 | 180 | 0.902 | 0.094 | 0.06 |
| Strict Model | 660.398 | 194 | 0.888 | 0.097 | 0.062 |
| Strict Model RS9 | 646.559 | 193 | 0.891 | 0.096 | 0.062 |
| Strict Model RS9 + 13 | 633.111 | 192 | 0.894 | 0.095 | 0.062 |
Interpretation
- The RS is mostly invariant – the structure, loadings, intercepts, and most of the error variances are the same across men and women.
- However, two items show larger variances:
- RS9
- RS13
- Where, women show much larger variances on both of those questions.
- I keep interested in things.
- My life has meaning.
lavPredict on the items
predicted_scores <- lavPredict(strict.fit3, type = "ov")
table(res.data$Sex)
#>
#> Men Women
#> 244 266
predicted_scores <- as.data.frame(do.call(rbind, predicted_scores))
predicted_scores$Sex <- c(rep("Women", 266), rep("Men", 244))
predicted_scores$sum <- apply(predicted_scores[ , 1:14], 1, sum)
head(predicted_scores)
#> RS1 RS2 RS3 RS4 RS5 RS6 RS7 RS8
#> 1 4.398945 3.664178 3.685068 3.898936 3.267464 4.489343 4.369067 3.807156
#> 2 5.812096 5.401971 5.184889 5.632255 4.964156 6.209687 6.153074 5.514666
#> 3 6.517211 6.269071 5.933248 6.497123 5.810748 7.068081 7.043233 6.366655
#> 4 5.458156 4.966720 4.809240 5.198124 4.539199 5.778806 5.706248 5.086999
#> 5 4.051653 3.237102 3.316476 3.472960 2.850489 4.066555 3.930633 3.387523
#> 6 4.625009 3.942175 3.924997 4.176218 3.538887 4.764549 4.654457 4.080309
#> RS9 RS10 RS11 RS12 RS13 RS14 Sex sum
#> 1 3.686699 4.085209 3.896680 4.482787 4.262883 4.148736 Women 56.14315
#> 2 5.479791 5.769280 5.747900 6.125213 6.201545 6.033519 Women 80.23004
#> 3 6.374483 6.609575 6.671596 6.944727 7.168871 6.973961 Women 92.24858
#> 4 5.030689 5.347484 5.284240 5.713847 5.715984 5.561452 Women 74.19719
#> 5 3.246033 3.671336 3.441728 4.079148 3.786442 3.685536 Women 50.22361
#> 6 3.973543 4.354613 4.192822 4.745528 4.573014 4.450247 Women 59.99637
tapply(predicted_scores$sum, predicted_scores$Sex, mean)
#> Men Women
#> 63.34281 64.24733lavPredict on the factor scores
res.data$sum <- apply(res.data[ , 3:16], 1, sum)
tapply(res.data$sum, res.data$Sex, mean)
#> Men Women
#> 63.47131 64.10902
latent_means <- lavPredict(strict.fit3)
latent_means <- as.data.frame(do.call(rbind, latent_means))
latent_means$Sex <- c(rep("Women", 266), rep("Men", 244))
options(scipen = 999)
tapply(latent_means$RS, latent_means$Sex, mean)
#> Men Women
#> -0.0530675184545 -0.0000004953854
tapply(latent_means$RS, latent_means$Sex, mean) * #latent mean
tapply(res.data$sum, res.data$Sex, sd, na.rm = T) + #real sum
tapply(res.data$sum, res.data$Sex, mean, na.rm = T) #real sd
#> Men Women
#> 62.32949 64.10901Calculate your favorite stat
library(MOTE)
M <- tapply(predicted_scores$sum, predicted_scores$Sex, mean)
SD <- tapply(predicted_scores$sum, predicted_scores$Sex, sd)
N <- tapply(predicted_scores$sum, predicted_scores$Sex, length)
effect_size <- d.ind.t(M[1], M[2], SD[1], SD[2], N[1], N[2], a = .05)
effect_size$estimate
#> [1] "$d_s$ = -0.05, 95\\% CI [-0.22, 0.13]"
effect_size$statistic
#> [1] "$t$(508) = -0.54, $p$ = .587"